
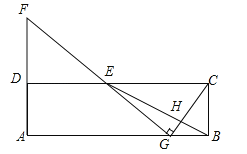
【题目】在矩形ABCD中,E为CD的中点,H为BE上的一点,![]() =3,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
=3,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
(1)求证:![]() ;
;
(2)若∠CGF=90°,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)根据相似三角形判定的方法,判断出△CEH∽△GBH,即可推得结论;
(2)作EM⊥AB于M,则EM=BC=AD,AM=DE,设DE=CE=3a,则AB=CD=6a,由(1)得:![]() =3,得出BG=
=3,得出BG=![]() CE=a,AG=5a,证明△DEF∽△GEC,由相似三角形的性质得出EGEF=DEEC,由平行线证出
CE=a,AG=5a,证明△DEF∽△GEC,由相似三角形的性质得出EGEF=DEEC,由平行线证出![]() =
=![]() ,得出EF=
,得出EF=![]() EG,求出EG=
EG,求出EG=![]() a,在Rt△EMG中,GM=2a,由勾股定理求出BC=EM=
a,在Rt△EMG中,GM=2a,由勾股定理求出BC=EM=![]() a,即可得出结果.
a,即可得出结果.
试题解析:(1)证明:∵四边形ABCD是矩形,∴CD∥AB,AD=BC,AB=CD,AD∥BC,∴△CEH∽△GBH,∴![]() .
.
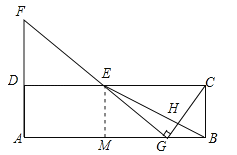
(2)解:作EM⊥AB于M,如图所示:
则EM=BC=AD,AM=DE,∵E为CD的中点,∴DE=CE,设DE=CE=3a,则AB=CD=6a,由(1)得:![]() =3,∴BG=
=3,∴BG=![]() CE=a,∴AG=5a,∵∠EDF=90°=∠CGF,∠DEF=∠GEC,∴△DEF∽△GEC,∴
CE=a,∴AG=5a,∵∠EDF=90°=∠CGF,∠DEF=∠GEC,∴△DEF∽△GEC,∴![]() ,∴EGEF=DEEC,∵CD∥AB,∴
,∴EGEF=DEEC,∵CD∥AB,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴EF=
,∴EF=![]() EG,∴EG
EG,∴EG![]() EG=3a3a,解得:EG=
EG=3a3a,解得:EG=![]() a,在Rt△EMG中,GM=2a,∴EM=
a,在Rt△EMG中,GM=2a,∴EM=![]() =
=![]() a,∴BC=
a,∴BC=![]() a,∴
a,∴![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
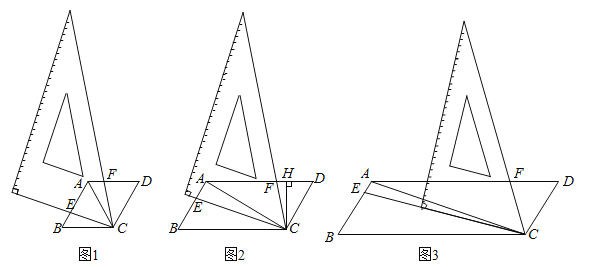
【题目】数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究
如图3,若AD=3AB,探究得:![]() 的值为常数t,则t= .
的值为常数t,则t= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB的边OB上的一点.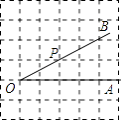
(1)过点P画OB的垂线,交OA于点C,
(2)过点P画OA的垂线,垂足为H,
(3)线段PH的长度是点P到的距离,线段是点C到直线OB的距离.
(4)因为直线外一点到直线上各点连接的所有线中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是(用“<”号连接)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com