
【题目】如图,矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=6,求AE的长。

【答案】AE的长为![]() .
.
【解析】试题分析:先根据折叠的性质得到∠DBC=∠DBE,再由AD∥BC得到∠DBC=∠BDE,则∠DBE=∠BDE,于是可判断BE=DE设AE=x,则DE=BE=8-x,然后在Rt△ABE中利用勾股定理得到x2+62=(8-x)2,再解方程即可.
试题解析:∵矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,
∴∠C′BD=∠CBD,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠EDB=∠CBD,
∴∠EDB=∠C′BD,
∴EB=ED,
设AE=x,则ED=AD﹣AE=8﹣x,BE=8﹣x,
在Rt△ABE中,
∵AB2+AE2=BE2,
∴62+x2=(8﹣x)2,解得x=![]() ,
,
即AE的长为![]() 。
。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】根据下列条件可列出一元一次方程的是( )
A. a与1的和的3倍
B. 甲数的2倍与乙数的3倍的和
C. a与b的差的20%
D. 一个数的3倍是5
查看答案和解析>>
科目:初中数学 来源: 题型:
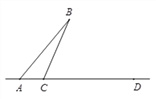
【题目】如图,线段AB,AD交于点A.C为直线AD上一点(不与点A,D重合).过点C在BC的右侧作射线CE⊥BC,过点D作直线DF∥AB,交CE于点G(G与D不重合).
(1)如图1,若点C在线段AD上,且∠BCA为钝角.
①按要求补全图形;②判断∠B与∠CGD的数量关系,并证明.
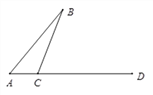
(2)若点C在线段DA的延长线上,请直接写出∠B与∠CGD的数量关系 ;
附加题(2分).
请你结合28题的题意提出一个新的拓展问题 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=2(x﹣1)2+3的顶点坐标是( )
A. (1,3) B. (1,﹣3) C. (﹣1,3) D. (﹣1,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某综合实践小组为了了解本校学生参加课外读书活动的情况,随机抽取部分学生,调查其最喜欢的图书类别,并根据调查结果绘制成如下不完整的统计表与统计图:
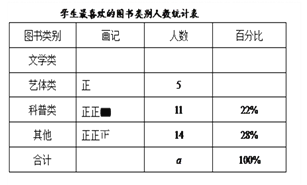
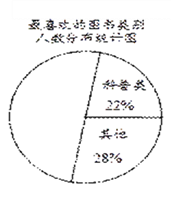

请结合图中的信息解答下列问题:
(1)随机抽取的样本容量a为 ;
(2)补全扇形统计图和条形统计图;
(3)已知该校有600名学生,估计全校最喜欢文学类图书的学生有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
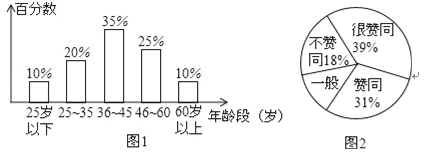
【题目】据报载,在“百万家庭低碳行,垃圾分类要先行”活动中,某地区对随机抽取的1000名公民的年龄段分布情况和对垃圾分类所持态度进行调查,并将调查结果分别绘成条形图(图1)、扇形图(图2).
(1)图2中所缺少的百分数是 ;
(2)这次随机调查中,如果公民年龄的中位数是正整数,那么这个中位数所在年龄段是 ____ (填写年龄段);
(3)这次随机调查中,年龄段是“25岁以下”的公民中“不赞成”的有5名,它占“25岁以下”人数的百分数是 ___ ;
(4)如果把所持态度中的“很赞同”和“赞同”统称为“支持”,那么这次被调查公民中“支持”的人有 ____名.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com