
【题目】如图,CA⊥AB,垂足为点A,AB=8,AC=4,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E离开点A后,运动______ 秒时,△DEB与△BCA全等.

【答案】0,2,6,8
【解析】
此题要分两种情况:①当E在线段AB上时,②当E在BN上,再分别分成两种情况AC=BE,AC=BE进行计算即可.
①当E在线段AB上,AC=BE时,△ACB≌△BED,
∵AC=4,
∴BE=4,
∴AE=84=4,
∴点E的运动时间为4÷2=2(秒);
②当E在BN上,AC=BE时,
∵AC=4,
∴BE=4,
∴AE=8+4=12,
∴点E的运动时间为12÷2=6(秒);
③当E在线段AB上,AB=EB时,△ACB≌△BDE,
这时E在A点未动,因此时间为0秒;
④当E在BN上,AB=EB时,△ACB≌△BDE,
AE=8+8=16,
点E的运动时间为16÷2=8(秒),
故答案为:0,2,6,8.


科目:初中数学 来源: 题型:
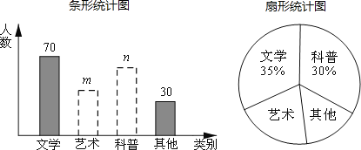
【题目】在“书香包河”读书活动中,学校准备购买一批课外读物,为使课外读物满足学生们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了______________名同学;
(2)条形统计图中,m=_________,n=__________;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AB=4,∠C=30°,点E、F分别是边AB、CD的中点,作DP∥AB交EF于点G,∠PDC=90°,求线段GF的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示的数a、点B表示数b,a、b满足|a﹣30|+(b+6)2=0.点O是数轴原点.
![]()
(1)点A表示的数为 ,点B表示的数为 ,线段AB的长为 .
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=2BC,则点C在数轴上表示的数为 .
(3)现有动点P、Q都从B点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到O点时,点Q才从B点出发,并以每秒3个单位长度的速度向右移动,且当点P到达A点时,点Q就停止移动,设点P移动的时间为t秒,问:当t为多少时,P、Q两点相距4个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.

解:∵∠1+∠2=180°(已知),
∠1+∠EFD=180°(邻补角定义),
∴∠2=∠EFD( )
∴AB∥EF(内错角相等,两直线平行)
∴∠ADE=∠3( )
∵∠3=∠B(已知)
∴∠ADE=∠B( )
∴ (同位角相等,两直线平行)
∴∠AED=∠C(两直线平行,同位角相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】移动公司为了方便学生上网查资料,提供了两种上网优惠方法:
A.计时制:0.08元/分钟;B.包月制:40元/月(只限一台电脑上网).
另外,不管哪种收费方式,上网时都得加收通讯费0.03元/分钟.
(1)设小明某月上网时间为x分钟,请分别用含x的式子表示出两种付费方式下小明应支付的费用;
(2)一个月上网时间为多少分钟时,两种方式付费一样多?
(3)如果一个月上网10小时,选择哪种方式更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其顶点Q落在线段AE上,定点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个边长为a(单位:cm)的正方形ABCD中,点E、M分别是线段AC,CD上的动点,连结DE并延长交正方形的边于点F,过点M作MN⊥DF于H,交AD于N.
(1)如图1,当点M与点C重合,求证:DF=MN;
(2)如图2,假设点M从点C出发,以1cm/s的速度沿CD向点D运动,点E同时从点A出发,以 ![]() cm/s速度沿AC向点C运动,运动时间为t(t>0);
cm/s速度沿AC向点C运动,运动时间为t(t>0);
①判断命题“当点F是边AB中点时,则点M是边CD的三等分点”的真假,并说明理由.
②连结FM、FN,△MNF能否为等腰三角形?若能,请写出a,t之间的关系;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com