
分析 先求出方程的解与不等式组的解集,再根据题目中的要求求出相应的k的值即可解答本题.
解答 解:$\frac{x}{{x}^{2}-1}+\frac{1}{x+1}=\frac{k}{1-{x}^{2}}$
方程两边同乘以(x+1)(x-1),得
x+(x-1)=-k
解得,x=$\frac{1-k}{2}$,
∵关于x的方程$\frac{x}{{x}^{2}-1}+\frac{1}{x+1}=\frac{k}{1-{x}^{2}}$的解为负数,
∴$\frac{1-k}{2}<0$,
解得k>1,
解不等式组$\left\{\begin{array}{l}{x-2>2}\\{x-k≤1}\end{array}\right.$,得4<x≤k+1,
∴使关于x的不等式组$\left\{\begin{array}{l}{x-2>2}\\{x-k≤1}\end{array}\right.$只有一个整数解的整数k的值为4,
故答案为:4.
点评 本题考查分式方程的解、一元一次不等式组的整数解,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:解答题
 如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
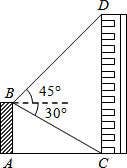 如图,某同学站在低楼AB上观察高楼CD,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,经过查找资料了解到楼房CD的高度为51.7m,求楼间距AC.($\sqrt{3}≈1.7$)
如图,某同学站在低楼AB上观察高楼CD,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,经过查找资料了解到楼房CD的高度为51.7m,求楼间距AC.($\sqrt{3}≈1.7$)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com