
分析 根据已知得出$(\sqrt{2}-1+\sqrt{3}-\sqrt{2}+…+\sqrt{2009}-$$\sqrt{2008})(\sqrt{2009}+1)$$(\sqrt{2009}+1)$,推出$(\sqrt{2009}-1)(\sqrt{2009}+1)$,根据平方差公式求出即可.
解答 解:原式=$(\sqrt{2}-1+\sqrt{3}-\sqrt{2}+…+\sqrt{2009}-$$\sqrt{2008})(\sqrt{2009}+1)$$(\sqrt{2009}+1)$=$(\sqrt{2009}-1)(\sqrt{2009}+1)$=2008.
点评 本题考查了分母有理化的应用,解此题的关键是根据题目的结果找出规律,题目比较好,有一定的难度.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
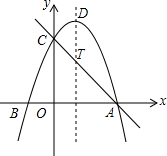 已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(3、0)和点B(-1,0),与y轴交于点C,抛物线顶点为点D.
已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(3、0)和点B(-1,0),与y轴交于点C,抛物线顶点为点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
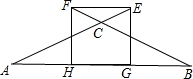 如图,△ABC中,CA=CB,E、F分别在AC、AB的延长线上,且CE=CF,EG⊥AB于G,FH⊥AB于H,连接EF.
如图,△ABC中,CA=CB,E、F分别在AC、AB的延长线上,且CE=CF,EG⊥AB于G,FH⊥AB于H,连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
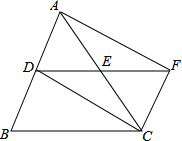 如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,连接DE并延长到点F,使EF=DE,连接AF、CF.求证:四边形ADCF是矩形.
如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,连接DE并延长到点F,使EF=DE,连接AF、CF.求证:四边形ADCF是矩形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com