
分析 (1)将1m转化成106μm,再除以每颗花粉的直径可得;
(2)根据a2+b2=[(a+b)2+(a-b)2]÷2、ab=[(a+b)2-(a-b)2]÷4代入计算可得;
(3)将103m-2n+1转化成(10m)3÷(10n)2×10,代入计算可得.
解答 解:(1)106÷50=2×104,
答:需2×104颗这样的花粉颗粒紧密排成一列的长度为1米;
(2)∵(a+b)2=7,(a-b)2=3,
∴a2+b2=[(a+b)2+(a-b)2]÷2=(7+3)÷2=5;
ab=[(a+b)2-(a-b)2]÷4=(7-3)÷4=1;
(3)当10m=4,10n=5时,
103m-2n+1=103m÷102n×10
=(10m)3÷(10n)2×10
=43÷52×10
=$\frac{128}{5}$.
点评 本题主要考查整式的混合运算能力,熟练掌握整式混合运算的法则、运算顺序及完全平方公式是关键.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,二次函数y=x2-3x的图象与x轴相交于O、A两点.
如图,在平面直角坐标系xOy中,二次函数y=x2-3x的图象与x轴相交于O、A两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
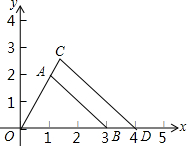 如图,△AOB以O为位似中心,扩大到△COD,各点的坐标分别为A(1,2),B(3,0),D(4,0),求点C的坐标,并求出四边形ABDC的面积.
如图,△AOB以O为位似中心,扩大到△COD,各点的坐标分别为A(1,2),B(3,0),D(4,0),求点C的坐标,并求出四边形ABDC的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
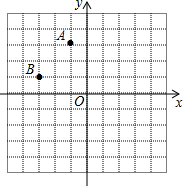 如图,平面直角坐标系中A(-1,3),B(-3,1)
如图,平面直角坐标系中A(-1,3),B(-3,1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则y的最大值是( )
如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则y的最大值是( )| A. | 36 | B. | 18 | C. | 20 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com