
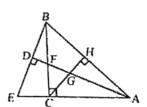
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,与BC相交于点F,过点B作BE⊥AD于点D,交AC延长线于点E,过点C作CH⊥AB于点H,交AF于点G,则下列结论:![]() ⑤
⑤![]() ;正确的有( )个.
;正确的有( )个.
A.1B.2C.3D.4
【答案】D
【解析】
①②正确,只要证明△BCE≌△ACF,△ADB≌△ADE即可解决问题;
③正确,只要证明GB=GA,得到△BDG是等腰直角三角形,即可得到;
④正确,求出∠CGF=67.5°=∠CFG,则CF=CG=CE,然后AE=AC+CE=BC+CG,即可得到结论;
⑤错误,作GM⊥AC于M.利用角平分线的性质定理即可证明;
解:∵AD⊥BE,
∴∠FDB=∠FCA=90°,
∵∠BFD=∠AFC,
∴∠DBF=∠FAC,
∵∠BCE=∠ACF=90°,BC=AC,
∴△BCE≌△ACF,
∴EC=CF,AF=BE,故①正确,
∵∠DAB=∠DAE,AD=AD,∠ADB=∠ADE=90°,
∴△ADB≌△ADE,
∴BD=DE,
∴AF=BE=2BD,故②正确,
如图,连接BG,
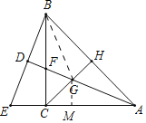
∵CH⊥AB,AC=AB,
∴BH=AH,∠BHG=∠AHG=90°
∵HG=HG,
∴△AGH≌△BGH,
∴BG=AG,∠GAH=∠GBH=22.5°,
∴∠DGB=∠GAH+∠GBH=45°,
∴△BDG是等腰直角三角形,
∴BD=DG=DE;故③正确;
由△ACH是等腰直角三角形,
∴∠ACG=45°,
∴∠CGF=45°+22.5°=67.5°,
∵∠CFG=∠DFB=90°-22.5°=67.5°,
∴∠CGF=∠CFG,
∴CG=CF,
∵AB=AE,BC=AC,CE=CF=CG,
又∵AE=AC+CE,
∴AB=BC+CG,故④正确;
作GM⊥AC于M,

由角平分线性质,GH=GM,
∴△AGH≌△AGM(HL),
∴△AGH的面积与△AGM的面积相等,
故⑤错误;
综合上述,正确的结论有:①②③④;
故选择:D.


科目:初中数学 来源: 题型:
【题目】① 如图(1),直线l上有2个点,则图中有2条可用图中字母表示的射线:A1A2、A2A1,有1条线段:A1A2;
② 如图(2),直线l上有3个点,则图中有几条可用图中字母表示的射线,有几条线段,并分别用图中字母表示出来;
③ 如图(3),直线l上有n个点,则图中有多少条可用图中字母表示的射线,有多少条线段,分别用含n的代数式表示出来;
④ 应用(3)中发现的规律解决问题:某校七年级共有8个班进行足球比赛,准备进行循环赛(即每两队之间赛一场),预计全部赛完共需多少场比赛?
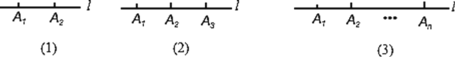
查看答案和解析>>
科目:初中数学 来源: 题型:
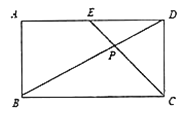
【题目】学完《平面直角坐标系》和《一次函数》这两章后,老师布置了这样一道思考题:已知:如图,在长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,
的中点,![]() 和
和![]() 相交于点
相交于点![]() .求
.求![]() 的面积.小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:以
的面积.小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:以![]() 所在的直线为
所在的直线为![]() 轴,以
轴,以![]() 所在的直线为
所在的直线为![]() 轴建立适当的平面直角坐标系,写出图中一些点坐标.根据一次函数的知识求出点
轴建立适当的平面直角坐标系,写出图中一些点坐标.根据一次函数的知识求出点![]() 的坐标,从而求得
的坐标,从而求得![]() 的面积.请你按照小明的思路解决这道思考题.
的面积.请你按照小明的思路解决这道思考题.
查看答案和解析>>
科目:初中数学 来源: 题型:
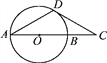
【题目】如图所示,D是半径为R的⊙O上一点,过点D作⊙O的切线交直径AB的延长线于点C,下列四个条件:①AD=CD;②∠A=30°;③∠ADC=120°;④DC=![]() R.其中能使得BC=R的有________(填序号).
R.其中能使得BC=R的有________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点 A(4,0),点 B 是 y 轴正半轴上一点,如图 1,以 AB 为直角边作等腰直角三角形 ABC ABC 90.
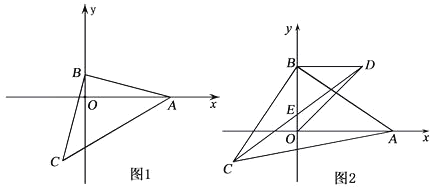
(1)若 AC 6,求点B 的坐标;
(2)当点B 坐标为(0,1)时,求点C 的坐标;
(3)如图 2,以 OB 为直角边作等腰直角△OBD,点D在第一象限,连接CD交 y 轴于点E.在点 B 运动的过程中,BE 的长是否发生变化?若不变,求出 BE 的长;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
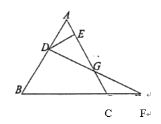
【题目】如图,在边长为1的等边△ABC的边AB取一点D,过点D作DE⊥AC于点E,在BC延长线取一点F,使CF=AD,连接DF交AC于点G,则EG的长为________
查看答案和解析>>
科目:初中数学 来源: 题型:
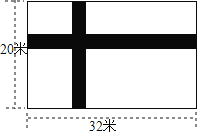
【题目】如图所示,宽为20米,长为32米的长方形地面上,修筑宽度为x米的两条互相垂直的小路,余下的部分作为耕地,如果要在耕地上铺上草皮,选用草皮的价格是每平米a元,
(1)求买草皮至少需要多少元?(用含a,x的式子表示)
(2)计算a=40,x=2时,草皮的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,记千位上和百位上的数字之和为![]() ,十位上和个位上的数字之和为
,十位上和个位上的数字之和为![]() ,如果
,如果![]() ,那么称这个四位数为“和平数”.
,那么称这个四位数为“和平数”.
例如:1423,![]() ,
,![]() ,因为
,因为![]() ,所以1423是“和平数”.
,所以1423是“和平数”.
(1)直接写出:最小的“和平数”是 ,最大的“和平数”是 ;
(2)将一个“和平数”的个位上与十位上的数字交换位置,同时,将百位上与千位上的数字交换位置,称交换前后的这两个“和平数”为一组“相关和平数”.
例如:1423与4132为一组“相关和平数”
求证:任意的一组“相关和平数”之和是1111的倍数.
(3)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的有( )
①如果等腰三角形的底角为15°,那么腰上的高是腰长的一半;
②三角形至少有一个内角不大于60°;
③连结任意四边形各边中点形成的新四边形是平行四边形;
④十边形内角和为1800°.
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com