
分析 (1)根据方程的系数结合根的判别式,可得△=(k-1)2≥0,由此可证出方程总有两个实数根;
(2)利用分解因式法解一元二次方程,可得出x1=2、x2=k+1,根据方程有一根小于1,即可得出关于k的一元一次不等式,解之即可得出k的取值范围.
解答 (1)证明:∵在方程x2-(k+3)x+2k+2=0中,△=[-(k+3)]2-4×1×(2k+2)=k2-2k+1=(k-1)2≥0,
∴方程总有两个实数根.
(2)解:∵x2-(k+3)x+2k+2=(x-2)(x-k-1)=0,
∴x1=2,x2=k+1.
∵方程有一根小于1,
∴k+1<1,解得:k<0,
∴k的取值范围为k<0.
点评 本题考查了根的判别式、因式分解法解一元二次方程以及解一元一次不等式,解题的关键是:(1)牢记“当△≥0时,方程有两个实数根”;(2)利用因式分解法解一元二次方程结合方程一根小于1,找出关于k的一元一次不等式.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:解答题
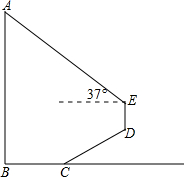 cos37°≈$\frac{4}{5}$,tan37°≈$\frac{3}{4}$.计算结果保留根号)
cos37°≈$\frac{4}{5}$,tan37°≈$\frac{3}{4}$.计算结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 4 | 3 | 5 | 32+42=52 |
| 6 | 8 | 10 | 62+82=102 |
| 8 | 15 | 17 | 82+152=172 |
| 10 | 24 | 26 | 102+242=262 |
| … | … | … | … |
| 60 | x | y | 602+x2=y2 |
| … | … | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
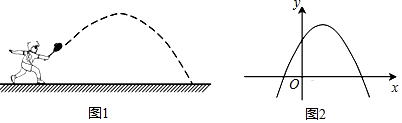
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com