
【题目】如图,数轴上的点A,B,C,D,E表示连续的五个整数,对应的数分别为a,b,c,d,e.
(1)若a=-3,则e = ;
(2)若a+e=0,则代数式b+c+d= ;
(3)若d是最大的负整数,求代数式![]() 的值(写出求解过程).
的值(写出求解过程).
(4)若e=4,F也为数轴上一点,且BE=2FE,则F表示的数为 ;
![]()
【答案】(1)1; (2) 0; (3)0; (4) 2.5或5.5.
【解析】
(1)根据数轴的特点,即可得解;
(2)根据已知条件,可判定A和E、B和D到C的距离相等,则可得解;
(3)首先判定出d=-1,则a、b、c、e便可得知,进而得解;
(4)根据已知条件,可得出BE,即可得解.
(1)∵a=-3,a,b,c,d,e表示连续的五个整数
∴e =1
(2)∵a+e=0,
∴A和E、B和D到C的距离相等,
∴b+c+d=0
(3)根据题意,得d=-1
∴a=-4,b=-3,c=-2,e=0
∴![]() =
=![]() =0
=0
(4)根据已知条件,得BE=3
∵BE=2FE,
∴FE=1.5
∵E表示的数是4
∴若F在E的左边,则F表示的数是2.5;
若F在E的右边,则F表示的数是5.5;
∴F表示的数为2.5或5.5


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:
【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O 中,AB为直径,CD为⊙O的切线,交AB的延长线于点D,∠D=30°.(1)求∠A的度数;(2)若点F在⊙O上,CF⊥AB,垂足为E,CF=4![]() ,求图中阴影部分的面积.(结果保留π)
,求图中阴影部分的面积.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定,若关于![]() 的一元一次方程
的一元一次方程![]() 的解为
的解为![]() ,则称该方程为“奇异方程”.例如:
,则称该方程为“奇异方程”.例如:![]() 的解为
的解为![]() ,则该方程
,则该方程![]() 是“奇异方程”.请根据上述规定解答下列问题:
是“奇异方程”.请根据上述规定解答下列问题:
(Ⅰ)判断方程![]() ________(回答“是”或“不是”)“奇异方程”;
________(回答“是”或“不是”)“奇异方程”;
(Ⅱ)若![]() ,有符合要求的“奇异方程”吗?若有,求
,有符合要求的“奇异方程”吗?若有,求![]() 的值;若没有,请说明理由.
的值;若没有,请说明理由.
(Ⅲ)若关于![]() 的一元一次方程
的一元一次方程![]() 和
和![]() 都是“奇异方程”,求代数式
都是“奇异方程”,求代数式![]() +
+![]()
![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据爱因斯坦的相对论可知,任何物体的运动速度不能超过光速(3×105km/s),因为一个物体达到光速需要无穷多的能量,并且时光会倒流,这在现实中是不可能的.但我们可让一个虚拟物超光速运动,例如:直线l,m表示两条木棒相交成的锐角的度数为10°,它们分别以与自身垂直的方向向两侧平移时,它们的交点A也随着移动(如图箭头所示),如果两条直线的移动速度都是光速的0.2倍,则交点A的移动速度是光速的_____倍.(结果保留两个有效数字).
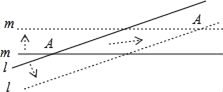
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】篝火晚会前夕,德强学校附近一超市从厂家购进了甲、乙两种发光道具,甲种道具的每件进价比乙种道具的每件进价少![]() 元.若购进甲种道具
元.若购进甲种道具![]() 件,乙种道具
件,乙种道具![]() 件,需要
件,需要![]() 元.
元.
(1)求甲、乙两种道具的每件进价分别是多少元?
(2)若该超市从厂家购进了甲乙两种道具共![]() 件,所用资金恰好为
件,所用资金恰好为![]() 元.在销售时,甲种
元.在销售时,甲种
道具的每件售价为![]() 元,要使得这
元,要使得这![]() 件道具所获利润率为
件道具所获利润率为![]() ,乙道具的每件售价为多少元?
,乙道具的每件售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任到一点P(点A除外),过点P作EF∥AB,分别交AC、BC于点E、F,作PQ∥AC,交AB于点Q,连接QE与AD相交于点G.
(1)求证:四边形AQPE是菱形.
(2)四边形EQBF是平行四边形吗?若是,请证明;若不是,请说明理由.
(3)直接写出P点在EF的何处位置时,菱形AQPE的面积为四边形EQBF面积的一半.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点A,O,B表示的数分别为6,0,-4,动点P从A出发,以每秒6个单位的速度沿数轴向左匀速运动.
(1)当点P到点A的距离与点P到点B的距离相等时,点P在数轴上表示的数是 ;
(2)另一动点R从B出发,以每秒4个单位的速度沿数轴向左匀速运动,若点P、R同时出发,问点P运动多少时间追上点R?
(3)若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段MN的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com