
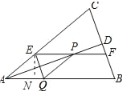
【题目】如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任到一点P(点A除外),过点P作EF∥AB,分别交AC、BC于点E、F,作PQ∥AC,交AB于点Q,连接QE与AD相交于点G.
(1)求证:四边形AQPE是菱形.
(2)四边形EQBF是平行四边形吗?若是,请证明;若不是,请说明理由.
(3)直接写出P点在EF的何处位置时,菱形AQPE的面积为四边形EQBF面积的一半.

【答案】(1)见解析;(2)结论:四边形EQBF是平行四边形.见解析;(3)当P为EF中点时,S菱形AEPQ=![]() S四边形EFBQ.
S四边形EFBQ.
【解析】
(1)先证出四边形AEPQ为平行四边形,关键是找一组邻边相等,由AD平分∠BAC和PE∥AQ可证∠EAP=∠EPA,得出AE=EP,即可得出结论;
(2)只要证明EQ∥BC,EF∥AB即可;
(3)S菱形AEPQ=EPh,S平行四边形EFBQ=EFh,若菱形AEPQ的面积为四边形EFBQ面积的一半,则EP=![]() EF,因此P为EF中点时,S菱形AEPQ=
EF,因此P为EF中点时,S菱形AEPQ=![]() S四边形EFBQ.
S四边形EFBQ.
(1)证明:∵EF∥AB,PQ∥AC,
∴四边形AEPQ为平行四边形,
∴∠BAD=∠EPA,
∵AB=AC,AD平分∠CAB,
∴∠CAD=∠BAD,
∴∠CAD=∠EPA,
∴EA=EP,
∴四边形AEPQ为菱形.
(2)解:结论:四边形EQBF是平行四边形.
∵四边形AQPE是菱形,
∴AD⊥EQ,即∠AGQ=90°,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC即∠ADB=90°,
∴EQ∥BC
∵EF∥QB,
∴四边形EQBF是平行四边形.
(3)解:当P为EF中点时, S菱形AEPQ=![]() S四边形EFBQ
S四边形EFBQ
∵四边形AEPQ为菱形,
∴AD⊥EQ,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴EQ∥BC,
又∵EF∥AB,
∴四边形EFBQ为平行四边形.
作EN⊥AB于N,如图所示:
∵P为EF中点
则S菱形AEPQ=EPEN=![]() EFEN=
EFEN=![]() S四边形EFBQ.
S四边形EFBQ.


科目:初中数学 来源: 题型:
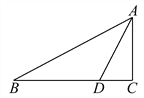
【题目】如图,已知在Rt△ABC中,∠C=90°,D是BC边上一点,AC=6,CD=3,∠ADC=α.
(1)试写出α的正弦、余弦、正切这三个函数值;
(2)若∠B与∠ADC互余,求BD及AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的点A,B,C,D,E表示连续的五个整数,对应的数分别为a,b,c,d,e.
(1)若a=-3,则e = ;
(2)若a+e=0,则代数式b+c+d= ;
(3)若d是最大的负整数,求代数式![]() 的值(写出求解过程).
的值(写出求解过程).
(4)若e=4,F也为数轴上一点,且BE=2FE,则F表示的数为 ;
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,德强学校初中部中考屡创佳绩,捷报频传.为了吸纳更多的优质生源,学校决定要新建一栋![]() 层的教学大楼,每层楼有
层的教学大楼,每层楼有![]() 间教室,进出这栋大楼共有
间教室,进出这栋大楼共有![]() 道门,其中两道正门大小相同,两道侧门大小相同,进楼前为了保证学生安全,对
道门,其中两道正门大小相同,两道侧门大小相同,进楼前为了保证学生安全,对![]() 道门进行了测试:正常情况下,当同时开启一道正门和两道侧门时,
道门进行了测试:正常情况下,当同时开启一道正门和两道侧门时,![]() 分钟可以通过
分钟可以通过![]() 名学生;当同时开启一道正门和一道侧门时
名学生;当同时开启一道正门和一道侧门时![]() 分钟可以通过
分钟可以通过![]() 名学生.
名学生.
(1)正常情况下,平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率将降低![]() ,安全检查规定,在紧急情况下全大楼的学生应在
,安全检查规定,在紧急情况下全大楼的学生应在![]() 分钟内通过这
分钟内通过这![]() 道门安全撤离.如果这栋教学楼每班预计招收45名学生,那么建造的这
道门安全撤离.如果这栋教学楼每班预计招收45名学生,那么建造的这![]() 道门是否符合安全规定?请说明理由.
道门是否符合安全规定?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.
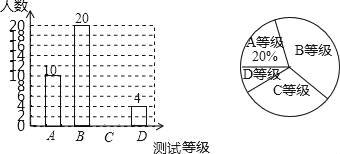
请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了 名学生?测试结果为C等级的学生数是 ,并补全条形图;
(2)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两名恰好都是男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市收府关于”垃圾不落地·市区更美丽”的主题宣传活动,某校随机调查了部分学生对垃圾分类知识的掌握情况.调查选项分为“A:非常了解,B:比较了解C:了解较少,D:不了解”四种,并将调查结果绘制成以下两幅不完整的统计图.
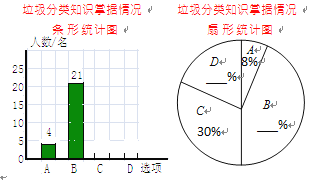
请根据图中提供的信息,解答下列问题:
(1)把两幅统计图补充完整;
(2)若该校学生数1000名,根据调查结果,估计该校“非常了解”与“比较了解”的学生共有________名;
(3)已知“非常了解”的4名男生和1名女生,从中随机抽取2名向全校做垃圾分类的知识交流,请用画树状图或列表的方法,求恰好抽到1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
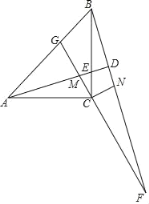
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点E是BC上一点(不与点B,C重合),点M是AE上一点(不与点A,E重合),连接并延长CM交AB于点G,将线段CM绕点C按顺时针方向旋转90°,得到线段CN,射线BN分别交AE的延长线和GC的延长线于D,F.
(1)求证:△ACM≌△BCN;
(2)求∠BDA的度数;
(3)若∠EAC=15°,∠ACM=60°,AC=![]() +1,求线段AM的长.
+1,求线段AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 、
、![]() 三地依次在同一直线上,
三地依次在同一直线上,![]() ,
,![]() 两地相距
两地相距![]() 千米,甲、乙两车分别从
千米,甲、乙两车分别从![]() ,
,![]() 两地同时出发,相向匀速行驶。行驶
两地同时出发,相向匀速行驶。行驶![]() 小时两车相遇,再经过
小时两车相遇,再经过![]() 小时,甲车到达
小时,甲车到达![]() 地,然后立即调头,并将速度提高
地,然后立即调头,并将速度提高![]() 后与乙车同向行驶,经过一段时间后两车同时到达
后与乙车同向行驶,经过一段时间后两车同时到达![]() 地,则
地,则![]() ,
,![]() 两地相距_____________千米.
两地相距_____________千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com