
【题目】近年来,德强学校初中部中考屡创佳绩,捷报频传.为了吸纳更多的优质生源,学校决定要新建一栋![]() 层的教学大楼,每层楼有
层的教学大楼,每层楼有![]() 间教室,进出这栋大楼共有
间教室,进出这栋大楼共有![]() 道门,其中两道正门大小相同,两道侧门大小相同,进楼前为了保证学生安全,对
道门,其中两道正门大小相同,两道侧门大小相同,进楼前为了保证学生安全,对![]() 道门进行了测试:正常情况下,当同时开启一道正门和两道侧门时,
道门进行了测试:正常情况下,当同时开启一道正门和两道侧门时,![]() 分钟可以通过
分钟可以通过![]() 名学生;当同时开启一道正门和一道侧门时
名学生;当同时开启一道正门和一道侧门时![]() 分钟可以通过
分钟可以通过![]() 名学生.
名学生.
(1)正常情况下,平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率将降低![]() ,安全检查规定,在紧急情况下全大楼的学生应在
,安全检查规定,在紧急情况下全大楼的学生应在![]() 分钟内通过这
分钟内通过这![]() 道门安全撤离.如果这栋教学楼每班预计招收45名学生,那么建造的这
道门安全撤离.如果这栋教学楼每班预计招收45名学生,那么建造的这![]() 道门是否符合安全规定?请说明理由.
道门是否符合安全规定?请说明理由.
【答案】(1)平均每分钟一道正门可以通过120名学生,平均每分钟一道侧门可以通过80名学生.(2)符合安全规定
【解析】
(1)本题的两个等量关系是:一道正门2分通过的人数+二道侧门2分通过的人数=560人.
一道正门4分通过的人数+一道正门4分通过的人数=800人.根据这两个等量关系可得出方程组,求出解.
(2)可根据(1)中求出的平均每分钟一道正门和一道侧门的通行量,算出8道门全部打开5分钟通过的人数,乘20%后同总人数进行比较,然后看看是否符合要求.
(1)由已知可设一道正门每分可通过x名,一道侧门每分可通过![]() 人;
人;
由题意得:
2x+4![]() =560,
=560,
解得:x=120
![]() =80
=80
答:平均每分钟一道正门可以通过120名学生,平均每分钟一道侧门可以通过80名学生.
(2)假设建造4道门符合安全, 紧急情况下4道门全部开放 ,则:学校总共有学生:45×8×4=1440
5分钟可以通过学生:5×(120×2+80×2)=2000
效率为20%,则通过学生为:2000×(1-20%)=1600
因为1600>1440 所以建造4道门,可以让学生在5分钟内撤离,符合安全规定.


科目:初中数学 来源: 题型:
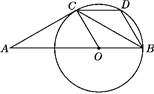
【题目】如图,△ABC是等腰三角形,且AC=BC,∠ACB=120°,在AB上取一点O,使OB=OC,以点O为圆心,OB为半径作圆,过点C作CD∥AB交⊙O于点D,连接BD.
(1)猜想AC与⊙O的位置关系,并证明你的猜想;
(2)试判断四边形BOCD的形状,并证明你的判断;
(3)已知AC=6,求扇形OBC所围成的圆锥的底面圆的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
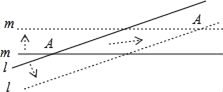
【题目】根据爱因斯坦的相对论可知,任何物体的运动速度不能超过光速(3×105km/s),因为一个物体达到光速需要无穷多的能量,并且时光会倒流,这在现实中是不可能的.但我们可让一个虚拟物超光速运动,例如:直线l,m表示两条木棒相交成的锐角的度数为10°,它们分别以与自身垂直的方向向两侧平移时,它们的交点A也随着移动(如图箭头所示),如果两条直线的移动速度都是光速的0.2倍,则交点A的移动速度是光速的_____倍.(结果保留两个有效数字).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】篝火晚会前夕,德强学校附近一超市从厂家购进了甲、乙两种发光道具,甲种道具的每件进价比乙种道具的每件进价少![]() 元.若购进甲种道具
元.若购进甲种道具![]() 件,乙种道具
件,乙种道具![]() 件,需要
件,需要![]() 元.
元.
(1)求甲、乙两种道具的每件进价分别是多少元?
(2)若该超市从厂家购进了甲乙两种道具共![]() 件,所用资金恰好为
件,所用资金恰好为![]() 元.在销售时,甲种
元.在销售时,甲种
道具的每件售价为![]() 元,要使得这
元,要使得这![]() 件道具所获利润率为
件道具所获利润率为![]() ,乙道具的每件售价为多少元?
,乙道具的每件售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
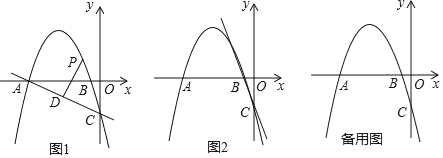
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2﹣
x2﹣![]() x﹣2
x﹣2![]() 与x轴交于A,B两点(点A在点B的左侧),交y轴于点C.
与x轴交于A,B两点(点A在点B的左侧),交y轴于点C.
(1)求直线AC的解析式;
(2)点P是直线AC上方抛物线上的一动点,过点P作PD⊥AC,垂足为D,当线段PD的长度最大时,点Q从点P出发,先以每秒1个单位的速度沿适当的路径运动到y轴上的点M处,再沿MC以每秒3个单位的速度运动到点C停止,当点Q在整个运动中所用时间t最少时,求点M的坐标;
(3)如图2,将△BOC沿直线BC平移,平移后B,O,C三点的对应点分别是B′,O′,C′,点S是坐标平面内一点,若以A,C,O′,S为顶点的四边形是菱形,请直接写出所有符合条件的点S的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任到一点P(点A除外),过点P作EF∥AB,分别交AC、BC于点E、F,作PQ∥AC,交AB于点Q,连接QE与AD相交于点G.
(1)求证:四边形AQPE是菱形.
(2)四边形EQBF是平行四边形吗?若是,请证明;若不是,请说明理由.
(3)直接写出P点在EF的何处位置时,菱形AQPE的面积为四边形EQBF面积的一半.

查看答案和解析>>
科目:初中数学 来源: 题型:
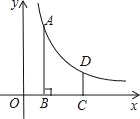
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D.
(x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D.
(1)点D的横坐标为_____(用户含m的代数式表示).
(2)当CD=![]() 时,求反比例函数所对应的函数表达式.
时,求反比例函数所对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
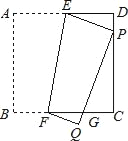
【题目】如图,已知正方形纸片ABCD的边长为2,将正方形纸片折叠,使顶点A落在边CD上的点P处(点P与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.
(1)观察操作结果,找到一个与△EDP相似的三角形,并证明你的结论;
(2)当点P位于CD中点时,你找到的三角形与△EDP周长的比是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com