
【题目】已知|x+2|+|1﹣x|=9﹣|y﹣5|﹣|1+y|,则x+y的最小值为_____,最大值为_____.
【答案】-3 6
【解析】
先将|x+2|+|1﹣x|=9﹣|y﹣5|﹣|1+y|化为|x+2|+|1﹣x|+|y﹣5|+|1+y|=9.分情况讨论可得当﹣2≤x≤1时,![]() 有最小值3,当﹣1≤y≤5时,
有最小值3,当﹣1≤y≤5时,![]() 有最小值6,从而根据|x+2|+|1﹣x|+|y﹣5|+|1+y|=9,可得x、y的取值范围,从而求得x+y的最小值和最大值.
有最小值6,从而根据|x+2|+|1﹣x|+|y﹣5|+|1+y|=9,可得x、y的取值范围,从而求得x+y的最小值和最大值.
解:因为|x+2|+|1﹣x|=9﹣|y﹣5|﹣|1+y|,
所以|x+2|+|1﹣x|+|y﹣5|+|1+y|=9,
当x≤-2时,![]() ,且当x=-2时,
,且当x=-2时,![]() 有最小值3,
有最小值3,
当﹣2<x<1时,![]() ,
,
当x≥1时,![]() ,且当x=1时,
,且当x=1时,![]() 有最小值3,
有最小值3,
故当﹣2≤x≤1时,![]() 有最小值3,
有最小值3,
当y≤﹣1时,![]() ,且当y=﹣1时,
,且当y=﹣1时,![]() 有最小值6,
有最小值6,
当﹣1<y<5时,![]() ,
,
当y≥5时,![]() ,且当y=5时,
,且当y=5时,![]() 有最小值6,
有最小值6,
故当﹣1≤y≤5时,![]() 有最小值6,
有最小值6,
所以,要使|x+2|+|1﹣x|+|y﹣5|+|1+y|=9,那么﹣2≤x≤1且﹣1≤y≤5,
故x+y最小值为﹣3,最大值为6.
故答案为:﹣3,6.


科目:初中数学 来源: 题型:
【题目】如图,已知⊙O 中,AB为直径,CD为⊙O的切线,交AB的延长线于点D,∠D=30°.(1)求∠A的度数;(2)若点F在⊙O上,CF⊥AB,垂足为E,CF=4![]() ,求图中阴影部分的面积.(结果保留π)
,求图中阴影部分的面积.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】篝火晚会前夕,德强学校附近一超市从厂家购进了甲、乙两种发光道具,甲种道具的每件进价比乙种道具的每件进价少![]() 元.若购进甲种道具
元.若购进甲种道具![]() 件,乙种道具
件,乙种道具![]() 件,需要
件,需要![]() 元.
元.
(1)求甲、乙两种道具的每件进价分别是多少元?
(2)若该超市从厂家购进了甲乙两种道具共![]() 件,所用资金恰好为
件,所用资金恰好为![]() 元.在销售时,甲种
元.在销售时,甲种
道具的每件售价为![]() 元,要使得这
元,要使得这![]() 件道具所获利润率为
件道具所获利润率为![]() ,乙道具的每件售价为多少元?
,乙道具的每件售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任到一点P(点A除外),过点P作EF∥AB,分别交AC、BC于点E、F,作PQ∥AC,交AB于点Q,连接QE与AD相交于点G.
(1)求证:四边形AQPE是菱形.
(2)四边形EQBF是平行四边形吗?若是,请证明;若不是,请说明理由.
(3)直接写出P点在EF的何处位置时,菱形AQPE的面积为四边形EQBF面积的一半.

查看答案和解析>>
科目:初中数学 来源: 题型:
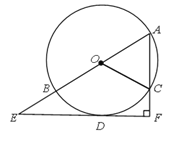
【题目】如图,AB是⊙O的直径,AC是弦,D是![]() 的中点,过点D作EF垂直于直线AC,垂足为F,交AB的延长线于点E.
的中点,过点D作EF垂直于直线AC,垂足为F,交AB的延长线于点E.
(1)求证:EF是⊙O的切线;
(2)若tanA=![]() ,AF=6,求⊙O的半径.
,AF=6,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
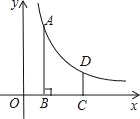
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D.
(x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D.
(1)点D的横坐标为_____(用户含m的代数式表示).
(2)当CD=![]() 时,求反比例函数所对应的函数表达式.
时,求反比例函数所对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接“六一”国际儿童节,某童装品牌专卖店准备购进甲、乙两种童装,这两种童装的进价和售价如下表:
价格 | 甲 | 乙 |
进价(元/件) | m | m+20 |
售价(元/件) | 150 | 160 |
如果用5000元购进甲种童装的数量与用6000元购进乙种童装的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种童装共200件的总利润(利润=售价﹣进价)不少于8980元,且甲种童装少于100件,问该专卖店有哪几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点A,O,B表示的数分别为6,0,-4,动点P从A出发,以每秒6个单位的速度沿数轴向左匀速运动.
(1)当点P到点A的距离与点P到点B的距离相等时,点P在数轴上表示的数是 ;
(2)另一动点R从B出发,以每秒4个单位的速度沿数轴向左匀速运动,若点P、R同时出发,问点P运动多少时间追上点R?
(3)若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段MN的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象.
(1)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当它们行驶7了小时时,两车相遇,求乙车速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com