
【题目】如图,等边三角形ABC的边长是2,D,E分别为AB,AC的中点,延长BC至点F,使CF= ![]() BC,连接DE,CD和EF.
BC,连接DE,CD和EF.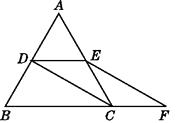
(1)求证:DE=CF;
(2)求EF的长.
【答案】
(1)证明:∵D,E分别为AB,AC的中点,
∴DE是△ABC的中位线.
∴DE= ![]() BC=1.
BC=1.
∵CF= ![]() BC=1,
BC=1,
∴DE=CF
(2)解:由(1)知DE是△ABC的中位线,
∴DE∥CF.
又∵DE=CF,
∴四边形CDEF是平行四边形.
∴CD=EF.
在等边三角形ABC中,D是AB的中点,
∴CD⊥AB,BD= ![]() AB=1.
AB=1.
∴CD= ![]() =
= ![]() .
.
∴EF= ![]()
【解析】(1)根据已知D,E分别为AB,AC的中点,可得出DE是△ABC的中位线,就可求出DE的长,再根据已知求出CF的长,就可证得结论。
(2)根据中位线定理得出DE∥CF,DE=CF,就可证得四边形CDEF是平行四边形,得出CD=FE,再根据等边三角形的三线合一的性质得出CD⊥AB,求出BD的长,然后根据勾股定理就可求出CD的长,即可得到EF的长。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=5cm,△ADC的周长为17cm,则BC的长为( )
A.7cm
B.10cm
C.12cm
D.22cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于比较38°15'和38.15°,下列说法正确的是( )
A.38°15'>38.15°B.38°15'<38.15°C.38°15'=38.15°D.无法比较
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC=BD,M,N分别是AB,CD的中点,MN分别交BD和AC于点E,F,对角线AC和BD相交于点G,则GE和GF相等吗?为什么?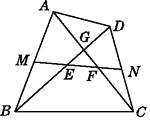
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年的信息技术结业考试,采用学生抽签的方式决定自己的考试内容.规定:每位考生先在三个笔试题(题签分别用代码B1、B2、B3表示)中抽取一个,再在三个上机题(题签分别用代码J1、J2、J3表示)中抽取一个进行考试.小亮在看不到题签的情况下,分别从笔试题和上机题中随机地抽取一个题签.
(1)用树状图或列表法表示出所有可能的结果;
(2)求小亮抽到的笔试题和上机题的题签代码的下标(例如“B1”的下标为“1”)为一个奇数一个偶数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com