
【题目】在等边![]() 中,点
中,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上,且有
的延长线上,且有![]() ,探究
,探究![]() 与
与![]() 的大小关系.
的大小关系.
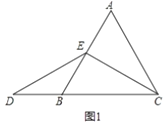
(1)如图1,当点![]() 为
为![]() 的中点时,如图1,确定线段
的中点时,如图1,确定线段![]() 与的
与的![]() 大小关系.请你直接写出结论:
大小关系.请你直接写出结论:![]() __________
__________![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”)
”)
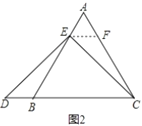
(2)特例启发,解答题目
解:如图2,![]() 与
与![]() 的大小关系是:
的大小关系是:![]() ___________
___________![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”)
”)
理由如下:如图2,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,(请你补充完成以下解答过程)
,(请你补充完成以下解答过程)
【答案】(1)=;(2)=.
【解析】
(1)根据等边三角形性质和等腰三角形的性质求出![]() =
=![]() ,求出DB=BE,进而得出AE=DB;
,求出DB=BE,进而得出AE=DB;
②根据题意结合平行线性质,利用全等三角形的判定,证得△BDE≌△FEC,求出DB=EF,又因为三角形AEF是等边三角形,AE=EF,进而得到AE=DB;
(1)∵![]() 为等边三角形,点
为等边三角形,点![]() 为
为![]() 的中点,
的中点,
∴![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
得出![]() ,
,
即有![]() ,
,
∴![]() ,
,
∴AE=DB.
(2)AE=DB,理由如下:
作EF//BC,交AB于E,AC于F,
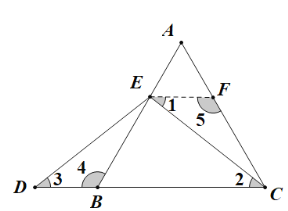
∵EF//BC,
∴∠AEF=∠ABC=60°,∠AFE=∠ACF=60°,∠1=∠2,
∴∠4=∠5=120°,
∵EC=ED,
∴∠2=∠3,
∴∠1=∠3,
在△BDE和△FEC中,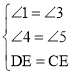 ,
,
∴△BDE≌△FEC,
∴DB=EF,
∵∠A=∠AEF=∠AFE=60°,
∴△AEF为等边三角形,
∴AE=EF,
∴AE=DB.
故答案为:(1)=;(2)=.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
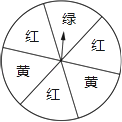
【题目】有一个转盘(如图所示),被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色.估计各事件的可能性大小,完成下列问题:
(1)可能性最大和最小的事件分别是哪个?(填写序号)
(2)将这些事件的序号按发生的可能性从小到大的顺序排列: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个布口袋里装着白、红、黑三种颜色的小球,它们除颜色之外没有任何其它区别,其中有白球3只、红球2只、黑球1只.袋中的球已经搅匀.
(1)闭上眼睛随机地从袋中取出1只球,求取出的球是黑球的概率;
(2)若取出的第1只球是红球,将它放在桌上,闭上眼睛从袋中余下的球中再随机地取出1只球,这时取出的球还是红球的概率是多少?
(3)若取出一只球,将它放回袋中,闭上眼睛从袋中再随机地取出1只球,两次取出的球都是白球概率是多少?(用列表法或树状图法计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班部分学生接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了如图①②两幅不完整的统计图,请根据图中的信息解答下列问题.
(1)九年级(1)班接受调查的学生共有多少名?
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
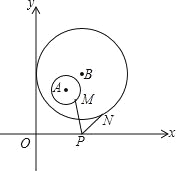
【题目】如图,平面直角坐标系中,分别以点A(2,3)、点B(3,4)为圆心,以1、3为半径作⊙A、⊙B,M,N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
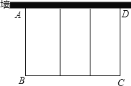
【题目】如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成三个大小相同的矩形羊圈.
(1)若羊圈总面积为400平方米,求羊圈的边长AB, BC各为多少米?
(2) 保持羊圈的基本结构,求羊圈总面积最大可以是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用无刻度的直尺按要求作图,请保留画图痕迹,不需要写作法。
(1)在8×6的正方形网格中,请用无刻度直尺画一个![]() 与
与![]() 面积相等,顶点在格点上 .(画出一个满足条件即可)
面积相等,顶点在格点上 .(画出一个满足条件即可)
(2)在8×6的正方形网格中,请用无刻度直尺画一个与![]() 面积相等,且以
面积相等,且以![]() 为边的平行四边形,顶点在格点上.(画出一个满足条件即可)
为边的平行四边形,顶点在格点上.(画出一个满足条件即可)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
(1)求证:AG与⊙O相切.
(2)若AC=6,AB=8,BE=3,求线段OE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com