
����Ŀ����֪����MON=40�㣬OEƽ�֡�MON����A��B��C�ֱ�������OM��OE��ON�ϵĶ��㣨A��B��C�����O�غϣ�������AC������OE�ڵ�D�����OAC= ![]() �㣮
�㣮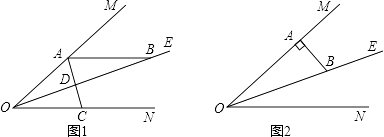
��1����ͼ1����AB//ON����١�ABO�Ķ������ڵ���BAD=��ABDʱ�� ![]() =���۵���BAD=��BDAʱ��
=���۵���BAD=��BDAʱ�� ![]() = ��
= ��
��2����ͼ2����AB��OM�����Ƿ����������x��ֵ��ʹ�á�ADB����������ȵĽǣ������ڣ����x��ֵ���������ڣ�˵������ ��
���𰸡�
��1��20�㣻120�㣻60��
��2�����ڣ�x��50��20��35��125
����������1��������ƽ���ߵ������Լ���ƽ���ߵĶ��壬�ɵâ١�ABO�Ķ������ڸ��ݡ�ABO����BAD�Ķ����Լ���AOB���ڽǺͣ��ɵ�x��ֵ����2������������������ۣ�AC��AB��࣬AC��AB�Ҳ࣬�ֱ�����������ڽǺͶ����Լ�ֱ�ǵĶ������ɵ�x��ֵ��
�����������ͼ1,�١ߡ�MON=36�� �� OEƽ�֡�MON��
���AOB=��BON=18 ��
��AB��ON��
���ABO=18��
�ڵ���BAD=��ABDʱ,��BAD=18�㣬
�ߡ�AOB+��ABO+��OAB=180�㣬
���OAC=180��18���3=126�㣻
����BAD=��BDAʱ,�ߡ�ABO=18�㣬
���BAD=81��,��AOB=18�㣬
�ߡ�AOB+��ABO+��OAB=180�㣬
���OAC=180��18��18��81��=63�㣬
�ʴ�Ϊ����18�㣻��126��63��
2����ͼ2������������x��ֵ��ʹ�á�ADB����������ȵĽǡ�
��AB��OM,��MON=36��OEƽ�֡�MON��
���AOB=18��,��ABO=72�㣬
�ٵ�AC��AB���ʱ��
����BAD=��ABD=72��,���OAC=90��72��=18�㣻
����BAD=��BDA=180��72��2=54��,���OAC=90��54��=36�㣻
����ADB=��ABD=72��,���BAD=36��,�ʡ�OAC=90��36��=54�㣻
�ڵ�AC��AB�Ҳ�ʱ��
�ߡ�ABE=108��,�������ε��ڽǺ�Ϊ180�㣬
��ֻ�С�BAD=��BDA=180��108��2=36��,���OAC=90��+36��=126��.
������������x=18��36��54��126ʱ����ADB����������ȵĽǡ�
�����⿼�������ε��ڽ�����̵��ۺ�Ӧ��.��ǵĹؼ��ǰ�δ֪�Ƿ����������У����������ε��ڽǺͶ�����ǣ���ת��Ϊ��֪���л������ϵ�Ľǣ���Щ��Ŀ������ת��Ϊ��֪�ǵĺͻ�������.


 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���ı��ν�ȥһ���Ǻ����������ǣ� ��
A. ������ B. ����� C. �ı��� D. ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A������Ϊ��3��-2�������A����ƽ��3����λ�������Ϊ�� ��
A. ��0��-2�� B. ��6��-2�� C. ��3��1�� D. ��3��-5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� ![]() �ֱ�ƽ��
�ֱ�ƽ�� ![]() �����
����� ![]() ���ڽ�
���ڽ� ![]() �����
����� ![]() .���½���: ��
.���½���: �� ![]() ;��
;�� ![]() ;��
;�� ![]() ƽ��
ƽ�� ![]() ;��
;�� ![]() ; ��
; �� ![]() ������ȷ�Ľ�����.
������ȷ�Ľ�����.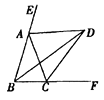
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ A��3x3+2x2��5x+7m+2��B��2x2+mx��3��������ʽ A+B ����һ�����������ʽ A+B �ij��������� ��
A. 16 B. 24 C. 34 D. 35
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�߳�Ϊ4��M��N�ֱ���BC��CD�ϵ��������㣬��M����BC���˶�ʱ������AM��MN��ֱ��
��1��֤����Rt��ABM ��Rt��MCN��
��2����BM=x������ABCN�����Ϊy����y��x֮��ĺ�����ϵʽ����M���˶���ʲôλ��ʱ���ı���ABCN�������������������
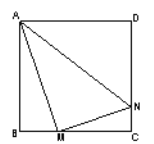 ��3����M���˶���ʲôλ��ʱRt��ABM��Rt��AMN�����ʱx��ֵ.
��3����M���˶���ʲôλ��ʱRt��ABM��Rt��AMN�����ʱx��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������������������ز��������������ɴ����ָ�������Ʒ�������ÿ�˷�5��������3�������ÿ�˷�6��������3���������������ؿ���������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com