
【题目】正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
(1)证明:Rt△ABM ∽Rt△MCN;
(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当M点运动到什么位置时,四边形ABCN的面积最大,并求出最大面积;
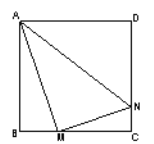 (3)当M点运动到什么位置时Rt△ABM∽Rt△AMN,求此时x的值.
(3)当M点运动到什么位置时Rt△ABM∽Rt△AMN,求此时x的值.
【答案】(1)、证明过程见解析;(2)、y=![]() ;最大值为10;(3)、BC的中点,x=2.
;最大值为10;(3)、BC的中点,x=2.
【解析】
试题分析:(1)、根据AM⊥MN得出∠CMN+∠AMB= 90°,根据Rt△ABM得出∠CMN=∠MAB,从而得出三角形相似;(2)、根据三角形相似得出CN与x的关系,然后根据梯形的面积计算法则得出函数解析式;(3)、根据要使三角形相似则需要满足![]() ,结合(1)中的条件得出BM=CM,即M为BC的中点.
,结合(1)中的条件得出BM=CM,即M为BC的中点.
试题解析:(1)在正方形ABCD中,AB=BC=CD=4,∠B=∠C =90°,
∵AM⊥MN ∴∠AMN= 90°. ∴∠CMN+∠AMB= 90°.
在Rt△ABM中,∠MAB+∠AMB=90°, ∴∠CMN=∠MAB. ∴Rt△AMN∽Rt△MCN;
(2)∵Rt△ABM∽Rt△MCN, ∴![]() ∴
∴![]() ∴CN=
∴CN=![]()
∴y=![]() =
=![]() =
=![]()
当x=2时,y取最大值,最大值为10;故当点肘运动到BC的中点时,四边形ABCN的面积最大,最大面积为10;
(3)∵∠B=∠AMN= 90°, ∴要使Rt△ABM∽Rt△AMN,必须 有![]()
由(1)知![]() ∴BM=MC
∴BM=MC
∴当点M运动到BC的中点时,Rt△ABM∽Rt△AMN,此时x=2


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.设∠OAC= ![]() °.
°.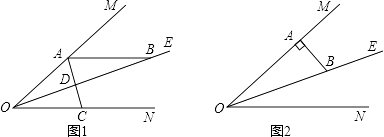
(1)如图1,若AB//ON,则①∠ABO的度数;②当∠BAD=∠ABD时, ![]() =;③当∠BAD=∠BDA时,
=;③当∠BAD=∠BDA时, ![]() = .
= .
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC在直角坐标平面内,三个顶点的坐标分别为A(-2,2)、B(-1,0)、C(0,1)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC关于y轴的轴对称图形△A1B1C1;
(2)以点O为位似中心,在网格内画出所有符合条件的△A2B2C2,使△A2B2C2 与△A1B1C1位似,且位似比为2:1;
(3)求△A1B1C1与△A2B2C2的面积比.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生物课题研究小组对附着在物体表面的三个微生物(课题组成员把他们分别标号为1,2,3)的生长情况进行观察记录,这三个微生物第一天各自一分为二,产生新的微生物(依次被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录),那么标号为1000的微生物会出现在( )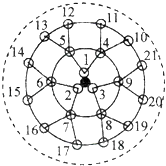
A.第7天
B.第8天
C.第9天
D.第10天
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有除颜色外均相同的8个黑球、4个白球和若干个红球.每次摇匀后随机摸出一个球,记下颜色后再放回袋中,通过大量重复摸球试验后,发现摸到红球的频率稳定于0.4,由此可估计袋中约有红球个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把四张形状大小完全相同的小长方形卡片不重叠地放在一个底面为长方形(长为a , 宽为b)的盒子底部,盒子底面未被卡片覆盖的部分用阴影表示,则这两块阴影部分小长方形周长的和为( ) 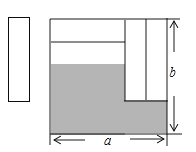
A.a+2b
B.4a
C.4b
D.2a+b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com