
【题目】已知,△ABC在直角坐标平面内,三个顶点的坐标分别为A(-2,2)、B(-1,0)、C(0,1)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC关于y轴的轴对称图形△A1B1C1;
(2)以点O为位似中心,在网格内画出所有符合条件的△A2B2C2,使△A2B2C2 与△A1B1C1位似,且位似比为2:1;
(3)求△A1B1C1与△A2B2C2的面积比.

【答案】见解析
【解析】
试题分析:关于原点位似的图形有两个,相似三角形的面积比等于相似比的平方.此题考查了位似变换以及轴对称变换。
(1)由△ABC关于y轴的轴对称图形△A1B1C1,根据轴对称的性质,可求得△A1B1C1各点的坐标,继而画出△A1B1C1;
(2)由△A2B2C2 与△A1B1C1位似,且位似比为2:1;根据位似的性质,可求得△A2B2C2各点的坐标,继而画出△A2B2C2;
(3)由相似三角形的面积比等于相似比的平方,即可求得△A1B1C1与△A2B2C2的面积比.
解 (1)如图:A1(2,2),B1(1,0),C1(0,1);
(2)如图:A1(4,4),B1(2,0),C1(0,2)或A1(-4,-4),B1(-2,0),C1(0,-2);
(3)∵△A2B2C2 与△A1B1C1位似,且位似比为2:1,
∴△A1B1C1与△A2B2C2的面积比=(![]() )2=
)2=![]() .
.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,线段A′B′是由线段AB经过平移得到的,已知点A(﹣2,1)的对应点为A′(3,﹣1),点B的对应点为B′(4,0),则点B的坐标为( )
A.(9,﹣2)
B.(﹣1,﹣2)
C.(9,2)
D.(﹣1,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 A=3x3+2x2﹣5x+7m+2,B=2x2+mx﹣3,若多项式 A+B 不含一次项,则多项式 A+B 的常数项是( )
A. 16 B. 24 C. 34 D. 35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B是线段EF上两点,EA:AB:BF=1:2:3,M,N分别为EA,BF的中点,且MN=8cm,则EF长( ) ![]()
A.9cm
B.10cm
C.11cm
D.12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
(1)证明:Rt△ABM ∽Rt△MCN;
(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当M点运动到什么位置时,四边形ABCN的面积最大,并求出最大面积;
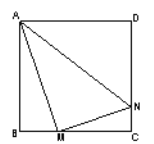 (3)当M点运动到什么位置时Rt△ABM∽Rt△AMN,求此时x的值.
(3)当M点运动到什么位置时Rt△ABM∽Rt△AMN,求此时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com