
【题目】如图1,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() 满足
满足![]() ,若对称轴在
,若对称轴在![]() 轴的右侧.
轴的右侧.
(1)求抛物线的解析式.
(2)如图![]() ,若点
,若点![]() 为线段
为线段![]() 上的一动点(不与
上的一动点(不与![]() 重合),分别以
重合),分别以![]() 、
、![]() 为斜边,在直线
为斜边,在直线![]() 的同侧作等腰直角三角形
的同侧作等腰直角三角形![]() 和
和![]() ,试确定
,试确定![]() 面积最大时
面积最大时![]() 点的坐标.
点的坐标.
(3)若![]() ,
,![]() 是抛物线上的两点,当
是抛物线上的两点,当![]() ,
,![]() 时,均有
时,均有![]() ,求
,求![]() 的取值范围.
的取值范围.


【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由二次函数与一元二次方程的关系,根据根与系数的关系得x+x=-2m,x·x=8m再联立![]() ,求解得m值,即可得出函数解析式;
,求解得m值,即可得出函数解析式;
(2)欲求△MNP的面积,确定△APM、△BNP是等腰直角三角形,即可求解;
(3)由(1)可知,函数的对称轴为:x=1,![]() 与
与![]() 关于对称轴对称,故其函数值相等,即可求解.
关于对称轴对称,故其函数值相等,即可求解.
解:(1) ![]() 与
与![]() 轴交于
轴交于![]() 和点
和点![]() ,
,
![]() 是方程
是方程![]() 的两个根
的两个根
![]() ,
,![]()
![]()
![]()
即![]()
解得![]() ,
,![]()
对称轴轴在![]() 轴的右侧
轴的右侧
![]()
![]()
(2)如图![]() ,
,![]() 和
和![]() 为等腰直角三角形
为等腰直角三角形
. ![]() .
.
![]()
![]() 为直角三角形
为直角三角形
令![]() ,解得:
,解得:![]() ,
,![]()
![]() ,
,![]() ,
,![]()
设![]() ,则
,则![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() 当
当![]() ,即
,即![]() 时,
时,![]() 最大,此时
最大,此时![]() ,所以
,所以![]()
(3)由函数![]() 可知,对称轴为
可知,对称轴为![]() ,则
,则![]() 与
与![]() 关于对称轴对称,故其函数值相等,都为
关于对称轴对称,故其函数值相等,都为![]()
又![]() ,
,![]() 时,均有
时,均有![]() ,
,
结合函数图象可得:
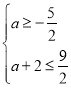 解得:
解得:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.

(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2,为什么?
(3)怎样围才能使围出的矩形场地面积最大?最大面积为多少?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:规定max(a,b)=![]() ,例如:max(﹣1,2)=2,max(3,3)=3.
,例如:max(﹣1,2)=2,max(3,3)=3.
感知:已知函数y=max(x+1,﹣2x+4)
(1)当x=3时,y=_____;
(2)当y=3时,x=______;
(3)当y随x的增大而增大时,x的取值范围为______;
(4)当﹣1≤x≤4时,y的取值范围为______;
探究:已知函数y=max(x+2,![]() )当直线y=m(m为常数)与函数y=max(x+2,
)当直线y=m(m为常数)与函数y=max(x+2,![]() )(﹣6<x≤3)的图象有两个公共点时,m的取值范围为_______;
)(﹣6<x≤3)的图象有两个公共点时,m的取值范围为_______;
拓展:已知函数y=max(﹣x2+2nx,﹣nx)(n为常数且n≠0),当![]() n﹣3≤x≤2时,随着x的增大,函数值y先减小后增大,直接写出n的取值范围.
n﹣3≤x≤2时,随着x的增大,函数值y先减小后增大,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,BE=FC,CF=2FD,AE、BF交于点G,连接AF,给出下列结论:①AE⊥BF; ②AE=BF; ③BG=![]() GE; ④S四边形CEGF=S△ABG,其中正确的个数为( )
GE; ④S四边形CEGF=S△ABG,其中正确的个数为( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着私家车的增多,“停车难”成了很多小区的棘手问题.某小区为解决这个问题,拟建造一个地下停车库.如图是该地下停车库坡道入口的设计示意图,其中,入口处斜坡![]() 的坡角为
的坡角为![]() ,水平线
,水平线![]() .根据规定,地下停车库坡道入口上方要张贴限高标志,以提醒驾驶员所驾车辆能否安全驶入.请求出限制高度为多少米,(结果精确到
.根据规定,地下停车库坡道入口上方要张贴限高标志,以提醒驾驶员所驾车辆能否安全驶入.请求出限制高度为多少米,(结果精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈尔滨市教育局以冰雪节为契机,在全市校园内开展多姿多彩的冰雪活动.某校为激发学生参与冰雪体育活动热情,开设了“滑冰、抽冰尜、冰球、冰壶、雪地足球”五个冰雪项目,并开展了以“我最喜欢的冰雪项目”为主题的调查活动,围绕“在滑冰、抽冰尜、冰球、冰壶、雪地足球中,你最喜欢的冰雪项目是什么?(每名学生必选且只选一个)”的问题在全校范围内随机抽取了部分学生进行问卷调查,根据调查结果绘制了如图所示的不完整的统计图.请根据统计图的信息回答下列问题:
(1)本次调查共抽取了多少名学生?
(2)求本次调查中,最喜欢冰球项目的人数,并补全条形统计图;
(3)若该中学共有1800名学生,请你估计该中学最喜欢雪地足球的学生约有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是![]() 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2![]() 时,阴影部分的面积为________
时,阴影部分的面积为________
查看答案和解析>>
科目:初中数学 来源: 题型:
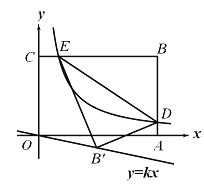
【题目】如图,平面直角坐标系![]() 中,矩形
中,矩形![]() 的边
的边![]() 、
、![]() 分别落在
分别落在![]() 、
、![]() 轴上,点
轴上,点![]() 坐标为
坐标为![]() ,反比例函数
,反比例函数![]() 的图象与
的图象与![]() 边交于点
边交于点![]() ,与
,与![]() 边交于点
边交于点![]() ,连结
,连结![]() ,将
,将![]() 沿
沿![]() 翻折至
翻折至![]() 处,点
处,点![]() 恰好落在正比例函数
恰好落在正比例函数![]() 图象上,则
图象上,则![]() 的值是
的值是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com