
【题目】如图,点E是ABCD的边AD的中点,BE与AC相交于点P,则S△APE:S△BCP= . 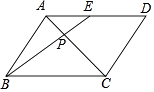
科目:初中数学 来源: 题型:
【题目】下列命题正确的个数是( )
①若代数式![]() 有意义,则x的取值范围为x≤1且x≠0.
有意义,则x的取值范围为x≤1且x≠0.
②我市生态旅游初步形成规模,2012年全年生态旅游收入为302 600 000元,保留三个有效数字用科学记数法表示为3.03×108元.
③若反比例函数![]() (m为常数),当x>0时,y随x增大而增大,则一次函数y=﹣2x+m的图象一定不经过第一象限.
(m为常数),当x>0时,y随x增大而增大,则一次函数y=﹣2x+m的图象一定不经过第一象限.
④若函数的图象关于y轴对称,则函数称为偶函数,下列三个函数:y=3,y=2x+1,y=x2中偶函数的个数为2个.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,从下列条件:①AB=BC,②∠ABC=90°, ③AC=BD,④AC⊥BD中,再选两个做为补充,使ABCD变为正方形.下面四种组
合,错误的是( )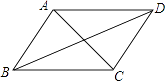
A.①②
B.①③
C.②③
D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
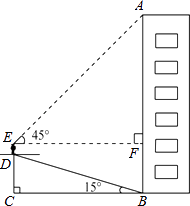
【题目】小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(计算结果精确到1m) (参考数据:sin15°= ![]() ,cos15°=
,cos15°= ![]() ,tan15°=
,tan15°= ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两个转盘分别被平均分成三个、四个扇形,分别转动A盘、B盘各一次.转动过程中,指针保持不动,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.请用列表或画树状图的方法,求两个转盘停止后指针所指区域内的数字之积小于6的概率. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是( ) 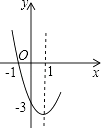
A.﹣1<x<4
B.x<﹣1或x>3
C.x<﹣1或x>4
D.﹣1<x<3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=ax2+bx+2的图象经过点A(﹣1,0),B(4,0)两点,与y轴交于点C. 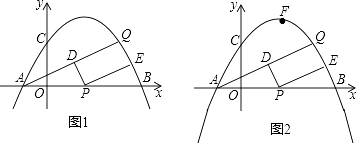
(1)求抛物线的解析式;
(2)若点Q(m,m﹣1)是抛物线上位于第一象限内的点,P是线段AB上的一个动点(不与A、B重合),经过点P分别作PD∥BQ交AQ于点D,PE∥AQ交BQ于点E. ①判断四边形PDQE的形状;并说明理由;
②连接DE,求出线段DE的长度范围;
③如图2,在抛物线上是否存在一点F,使得以P、F、A、C为顶点的四边形为平行四边形?若存在,求出点F和点P坐标;若不存在,说明理由.
(3)当r=2 ![]() 时,在P1(0,2),P2(﹣2,4),P3(4
时,在P1(0,2),P2(﹣2,4),P3(4 ![]() ,2),P4(0,2﹣2
,2),P4(0,2﹣2 ![]() )中,求可以成为正方形ABCD的“等距圆”的圆心的坐标?
)中,求可以成为正方形ABCD的“等距圆”的圆心的坐标?
(4)若点P坐标为(﹣3,6),则当⊙P的半径r为多长时,⊙P是正方形ABCD的“等距圆”.试判断此时⊙P与直线AC的位置关系?并说明理由.
(5)如图2,在正方形ABCD所在平面直角坐标系xOy中,正方形EFGH的顶点F的坐标为(6,2),顶点E、H在y轴上,且点H在点E的上方.若⊙P同时为上述两个正方形的“等距圆”,且与BC所在直线相切,求⊙P的圆心P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个命题中,属于真命题的共有( ) ①相等的圆心角所对的弧相等 ②若 ![]() =
= ![]()
![]() ,则a、b都是非负实数
,则a、b都是非负实数
③相似的两个图形一定是位似图形 ④三角形的内心到这个三角形三边的距离相等.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com