
【题目】如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO. 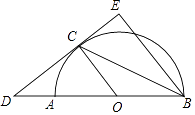
(1)求证:BC是∠ABE的平分线;
(2)若DC=8,⊙O的半径OA=6,求CE的长.
【答案】
(1)证明:∵DE是切线,
∴OC⊥DE,
∵BE∥CO,
∴∠OCB=∠CBE,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠CBE=∠CBO,
∴BC平分∠ABE.
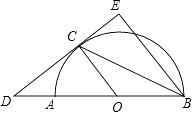
(2)在Rt△CDO中,∵DC=8,OC=0A=6,
∴OD= ![]() =10,
=10,
∵OC∥BE,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴EC=4.8.
【解析】(1)由BE∥CO,推出∠OCB=∠CBE,由OC=OB,推出∠OCB=∠OBC,可得∠CBE=∠CBO;(2)在Rt△CDO中,求出OD,由OC∥BE,可得 ![]() =
= ![]() ,由此即可解决问题;
,由此即可解决问题;
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( ) ①试验条件不会影响某事件出现的频率;
②在相同的条件下试验次数越多,就越有可能得到较精确的估计值,但各人所得的值不一定相同;
③如果一枚骰子的质量分布均匀,那么抛掷后每个点数出现的机会均等;
④抛掷两枚质量分布均匀的相同的硬币,出现“两个正面”、“两个反面”、“一正一反”的机会相同.
A.①②
B.②③
C.③④
D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与发现:
(1)若直线a1⊥a2,a2∥a3,则直线a1与a3的位置关系是__________,请说明理由.
(2)若直线a1⊥a2,a2∥a3,a3⊥a4,则直线a1与a4的位置关系是________.(直接填结论,不需要证明)
(3)现在有2 011条直线a1,a2,a3,…,a2 011,且有a1⊥a2,a2∥a3,a3⊥a4,a4∥a5…,请你探索直线a1与a2 011的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先填写表,通过观察后再回答问题:
a | … | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| … | 0.01 | x | 1 | y | 100 | … |
(1)表格中x= ,y= ;
(2)从表格中探究a与![]() 数位的规律,并利用这个规律解决下面两个问题:
数位的规律,并利用这个规律解决下面两个问题:
①已知![]() ≈3.16,则
≈3.16,则![]() ≈ ;
≈ ;
②已知![]() =8.973,若
=8.973,若![]() =897.3,用含m的代数式表示b,则b= ;
=897.3,用含m的代数式表示b,则b= ;
(3)试比较![]() 与a的大小.
与a的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某糕点厂中秋节前要制作一批盒装月饼,每盒装1个大月饼和7个小月饼,制作1个大月饼要用0.06kg面粉,1个小月饼要用0.015kg面粉,现共有面粉330kg,制作两种月饼各用多少kg面粉时,才能使生产的大小月饼刚好配套成盒?最多能生产多少盒月饼?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,点P是直径AB上的一点(不与A重合),过点P作AB的垂线交BC于点Q. 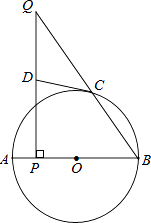
(1)在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD与⊙O的位置关系,并说明理由.
(2)若cosB= ![]() ,BP=6,AP=1,求QC的长.
,BP=6,AP=1,求QC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
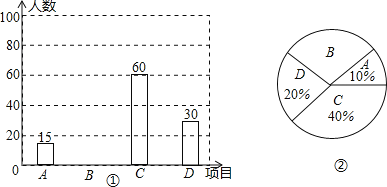
【题目】为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球.B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com