
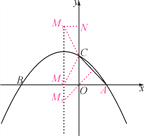
【题目】如图,已知抛物线y=-![]() x2-
x2-![]() x+2与x轴交于A,B两点,与y轴交于点C.
x+2与x轴交于A,B两点,与y轴交于点C.
(1)求点A,B,C的坐标;
(2)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.

【答案】(1) 点A的坐标为(2,0),点B的坐标为(-4,0),点C的坐标为(0,2);(2) 点M坐标为(-1,-1)或(-1,2+![]() )或(-1,2-
)或(-1,2-![]() ).
).
【解析】试题分析:(1)由抛物线y=-![]() x2-
x2-![]() x+2与x轴交于A,B两点,与y轴交于点C,分别令y=0与x=0,即可求得答案;
x+2与x轴交于A,B两点,与y轴交于点C,分别令y=0与x=0,即可求得答案;
(2)分别从M,C,A为顶点去分析求解即可求得答案.
试题解析:(1)令y=0,得-![]() x2-
x2-![]() x+2=0,
x+2=0,
∴x2+2x-8=0,解得x1=-4,x2=2,
∴点A的坐标为(2,0),点B的坐标为(-4,0),
令x=0,得y=2,
∴点C的坐标为(0,2);
(2)①当C为等腰三角形的顶角的顶点时,CM1=CA=2![]() ,CM2=CA,
,CM2=CA,
作M1N⊥OC于N,则M1N=1.
在Rt△CM1N中,CN=![]() =
=![]() ,
,
∴点M1坐标为(-1,2+![]() ),点M2坐标为(-1,2-
),点M2坐标为(-1,2-![]() );
);
②当M3为等腰三角形的顶角的顶点时,
易求直线AC的表达式为y=-x+2,
∴线段AC的垂直平分线为y=x与对称轴的交点为M3(-1,-1),
∴点M3的坐标为(-1,-1);
③当点A为等腰三角形的顶角的顶点的三角形不存在,
综上所述:点M坐标为(-1,-1)或(-1,2+![]() )或(-1,2-
)或(-1,2-![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
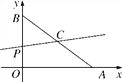
【题目】如图,在平面直角坐标系中,已知点A(4,0)和点B(0,3),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点P的坐标是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
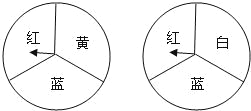
【题目】小明和小刚用如图所示的两个转盘做配紫色游戏,游戏规则是:分别旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色则可以配成紫色.此时小刚得1分,否则小明得1分.这个游戏规则对双方公平吗?请说明理由.若你认为不公平,如何修改规则才能使游戏对双方公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1,B1D1相交于点O.以点O为坐标原点,分别以OA1,OB1所在直线为x轴、y轴,建立如图所示的直角坐标系.以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,在x轴的正半轴上得到点A1,A2,A3,…,An,则点An的坐标为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,D、T是圆上的两点,且AT平分∠BAD,过点T作AD的延长线的垂线PQ,垂足为C.

(1)求证:PQ是⊙O的切线;
(2)已知⊙O的半径为2,若过点O作OE⊥AD,垂足为E,OE=![]() ,求弦AD的长.
,求弦AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A “明天降雨的概率是80%”表示明天有80%的时间降雨
B “抛一枚硬币正面朝上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上
C “彩票中奖的概率是1%”表示买100张彩票一定会中奖
D “抛一枚正方体骰子朝正面的数为奇数的概率是0.5“表示如果这个骰子抛很多很多次,那么平均每2次就有1次出现朝正面的数为奇数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com