
【题目】已知:a是﹣1,且a、b、c满足(c﹣6)2+|2a+b|=0,请回答问题:
(1)请直接写出b、c的值:b= , c=
(2)在数轴上,a、b、c所对应的点分别为A、B、C,点P为易动点,其对应的数为x,
(a)当点P在AB间运动(不包括A、B),试求出P点与A、B、C三点的距离之和.
(b)当点P从A点出发,向右运动,请根据运动的不同情况,化简式子:|x+1|﹣|x﹣2|+2|x﹣6|(请写出化简过程)![]()
【答案】
(1)2;6
(2)解:①∵PA=x﹣(﹣1)=x+1,PB=2﹣x,PC=6﹣x,
∴PA+PB+PC=x+1+2﹣x+6﹣x=9﹣x;|x+1|﹣|x﹣2|+2|x﹣6|(
②当﹣1≤x<2时,原式=x+1+x﹣2﹣2(x﹣6)=11;
当2≤x<6时,原式=x+1﹣(x﹣2)﹣2(x﹣6)=﹣2x+15;
当x≥6时,原式=x+1﹣(x﹣2)+2(x﹣6)=2x﹣9
【解析】解:(1)∵(c﹣6)2+|2a+b|=0,
∴c=6,2a+b=0,即b=﹣2a,
又∵a=﹣1,
∴b=2,
所以答案是:2,6;
【考点精析】本题主要考查了数轴和整式加减法则的相关知识点,需要掌握数轴是规定了原点、正方向、单位长度的一条直线;整式的运算法则:(1)去括号;(2)合并同类项才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图△ABC中,AB=AC=6,BC=4,∠A=40°. 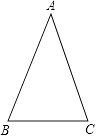
(1)用尺规作出边AB的垂直平分线交AB于点D,交AC于点E(不写作法,保留作图痕迹,并在图中标注字母).
(2)连接BE,求△EBC的周长和∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
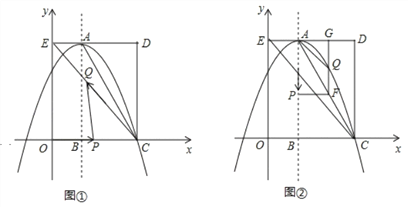
【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)填空:点A坐标为 ;抛物线的解析式为 .
(2)在图1中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图2中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示为某汽车行驶的路程S(km)与时间t(min)的函数关系图,观察图中所提供的信息解答下列问题: 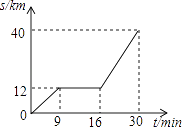
(1)汽车在前9分钟内的平均速度是多少?
(2)汽车中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com