
【题目】请你说明:一个三位数的百位上的数字与个位上的数字交换位置后,新数与原数之差能被99整除.
 核心素养学练评系列答案
核心素养学练评系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+b﹣2|+ ![]() =0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D.
=0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D. 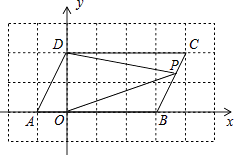
(1)请直接写出A、B、C、D四点的坐标并在坐标系中画出点A、B、C、D,连接AC,BD,CD.
(2)点E在坐标轴上,且S△BCE=S四边形ABDC , 求满足条件的点E的坐标.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在线段BD上移动时(不与B,D重合)证明: ![]() 是个常数.
是个常数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD. 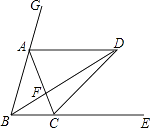
(1)求证:①AB=AD;②CD平分∠ACE.
(2)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:a是﹣1,且a、b、c满足(c﹣6)2+|2a+b|=0,请回答问题:
(1)请直接写出b、c的值:b= , c=
(2)在数轴上,a、b、c所对应的点分别为A、B、C,点P为易动点,其对应的数为x,
(a)当点P在AB间运动(不包括A、B),试求出P点与A、B、C三点的距离之和.
(b)当点P从A点出发,向右运动,请根据运动的不同情况,化简式子:|x+1|﹣|x﹣2|+2|x﹣6|(请写出化简过程)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)16﹣23+24﹣17
(2)﹣23÷(﹣ ![]() )÷(﹣
)÷(﹣ ![]() )2
)2
(3)( ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )×(﹣18)
)×(﹣18)
(4)(﹣1)10﹣(﹣3)×| ![]() ﹣
﹣ ![]() |÷
|÷ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知△ABC和△EFC都是等边三角形,点E在线段AB上. 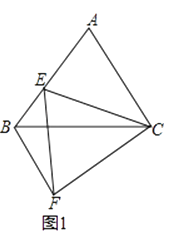
(1)求证:AE=BF,BF∥AC;
(2)若点D在直线AC上,且ED=EC(如图2),求证:AB=AD+BF; 
(3)在(2)的条件下,若点E改为在线段AB的延长线上,其它条件不变(如图3),请直接写出AB、AD、BF之间的数量关系. 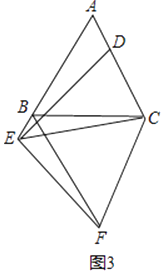
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:a是﹣1,且a、b、c满足(c﹣6)2+|2a+b|=0,请回答问题:
(1)请直接写出b、c的值:b= , c=
(2)在数轴上,a、b、c所对应的点分别为A、B、C,点P为易动点,其对应的数为x,
(a)当点P在AB间运动(不包括A、B),试求出P点与A、B、C三点的距离之和.
(b)当点P从A点出发,向右运动,请根据运动的不同情况,化简式子:|x+1|﹣|x﹣2|+2|x﹣6|(请写出化简过程)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=![]() ,则△EFC的周长为( )
,则△EFC的周长为( )
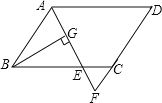
A. 11 B. 10 C. 9 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com