
【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD. 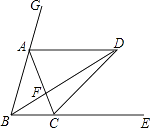
(1)求证:①AB=AD;②CD平分∠ACE.
(2)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.
【答案】
(1)解:①∵AD∥BE,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD;
②∵AD∥BE,
∴∠ADC=∠DCE,
由①知AB=AD,
又∵AB=AC,
∴AC=AD,
∴∠ACD=∠ADC,
∴∠ACD=∠DCE,
∴CD平分∠ACE
(2)解:∠BDC= ![]() ∠BAC,
∠BAC,
∵BD、CD分别平分∠ABE,∠ACE,
∴∠DBC= ![]() ∠ABC,∠DCE=
∠ABC,∠DCE= ![]() ∠ACE,
∠ACE,
∵∠BDC+∠DBC=∠DCE,
∴∠BDC+ ![]() ∠ABC=
∠ABC= ![]() ∠ACE,
∠ACE,
∵∠BAC+∠ABC=∠ACE,
∴∠BDC+ ![]() ∠ABC=
∠ABC= ![]() ∠ABC+
∠ABC+ ![]() ∠BAC,
∠BAC,
∴∠BDC= ![]() ∠BAC
∠BAC
【解析】(1)①根据平行线的性质得到∠ADB=∠DBC,由角平分线的定义得到∠ABD=∠DBC,等量代换得到∠ABD=∠ADB,根据等腰三角形的判定即可得到AB=AD;②根据平行线的性质得到∠ADC=∠DCE,由①知AB=AD,等量代换得到AC=AD,根据等腰三角形的性质得到∠ACD=∠ADC,求得∠ACD=∠DCE,即可得到结论;(2)根据角平分线的定义得到∠DBC= ![]() ∠ABC,∠DCE=
∠ABC,∠DCE= ![]() ∠ACE,由于∠BDC+∠DBC=∠DCE于是得到∠BDC+
∠ACE,由于∠BDC+∠DBC=∠DCE于是得到∠BDC+ ![]() ∠ABC=∠ACE,由∠BAC+∠ABC=∠ACE,于是得到∠DC+
∠ABC=∠ACE,由∠BAC+∠ABC=∠ACE,于是得到∠DC+ ![]() ∠ABC=
∠ABC= ![]() ∠ABC+
∠ABC+ ![]() ∠BAC,即可得到结论.
∠BAC,即可得到结论.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于E. 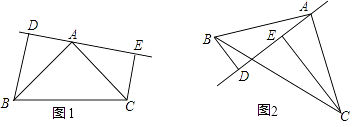
(1)若BC在DE的同侧(如图1)且AD=CE,请写出:BA和AC的位置关系 . (不必证明)
(2)若BC在DE的两侧(如图2)其他条件不变,请问(1)中AB与AC的位置关系还成立吗?若成立,写出证明过程;若不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,AB=AC=6,BC=4,∠A=40°. 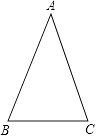
(1)用尺规作出边AB的垂直平分线交AB于点D,交AC于点E(不写作法,保留作图痕迹,并在图中标注字母).
(2)连接BE,求△EBC的周长和∠EBC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com