
分析 (1)根据题意求得顶点B的坐标,然后根据顶点公式即可求得m、n,从而求得y1的解析式;
(2)分两种情况讨论:当y1的解析式为y1=-x2-2x时,抛物线与x轴的交点是抛物线的顶点(-1,0),不合题意;
当y1=-x2-2x+8时,解-x2-2x+8=0求得抛物线与x轴的交点坐标,然后根据A的坐标和y2随着x的增大而增大,求得y1与y2都经过x轴上的同一点(-4,0),然后根据待定系数法求得即可.
解答 解:(1)∵抛物线y1=-x2+mx+n,直线y2=kx+b,y1的对称轴与y2交于点A(-1,5),点A与y1的顶点B的距离是4.
∴B(-1,1)或(-1,9),
∴-$\frac{m}{2×(-1)}$=-1,$\frac{4×(-1)n-{m}^{2}}{4×(-1)}$=1或9,
解得m=-2,n=0或8,
∴y1的解析式为y1=-x2-2x或y1=-x2-2x+8;
(2)①当y1的解析式为y1=-x2-2x时,抛物线与x轴交点是(0.0)和(-2.0),
∵y1的对称轴与y2交于点A(-1,5),
∴y1与y2都经过x轴上的同一点(-2,0),
把(-1,5),(-2,0)代入得$\left\{\begin{array}{l}{-k+b=5}\\{-2k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=5}\\{b=10}\end{array}\right.$,
∴y2=5x+10.
②当y1=-x2-2x+8时,解-x2-2x+8=0得x=-4或2,
∵y2随着x的增大而增大,且过点A(-1,5),
∴y1与y2都经过x轴上的同一点(-4,0),
把(-1,5),(-4,0)代入得$\left\{\begin{array}{l}{-k+b=5}\\{-4k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{5}{3}}\\{b=\frac{20}{3}}\end{array}\right.$;
∴y2=$\frac{5}{3}$x+$\frac{20}{3}$.
点评 本题考查了一次函数的性质,二次函数的性质,待定系数法求一次函数和二次函数的解析式,根据题意求得顶点坐标是解题的关键.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:选择题
| A. | 调查市场上某种白酒中塑化剂的含量 | |
| B. | 调查鞋厂生产的鞋底能承受的弯折次数 | |
| C. | 了解某火车的一节车厢内感染禽流感病毒的人数 | |
| D. | 了解某城市居民收看江苏卫视的时间 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5$\sqrt{5}$cm,且tan∠EFC=0.75,则矩形ABCD的周长为36cm.
如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5$\sqrt{5}$cm,且tan∠EFC=0.75,则矩形ABCD的周长为36cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
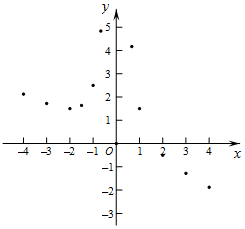 有这样一个问题:探究函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的图象与性质.
有这样一个问题:探究函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的图象与性质.| x | … | -4 | -3 | -2 | -$\frac{3}{2}$ | -1 | -$\frac{2}{3}$ | $\frac{2}{3}$ | 1 | 2 | 3 | 4 | … |
| y | … | $\frac{17}{8}$ | $\frac{31}{18}$ | $\frac{3}{2}$ | $\frac{59}{36}$ | $\frac{5}{2}$ | $\frac{29}{6}$ | $\frac{25}{6}$ | $\frac{3}{2}$ | -$\frac{1}{2}$ | -$\frac{23}{18}$ | m | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com