
如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求证:AD平分∠BAC;
(2)若∠BAC = 60°,OA = 2,求阴影部分的面积(结果保留 ).
).

 (1)证明:连接OD.
(1)证明:连接OD.
∵BC是⊙O的切线,D为切点,
∴OD⊥BC.············ 1分
又∵AC⊥BC,
∴OD∥AC,··········· 2分
∴∠ADO=∠CAD.········· 3分
又∵OD=OA,
∴∠ADO=∠OAD,···························· 4分
∴∠CAD=∠OAD,即AD平分∠BA C.····················· 5分
C.····················· 5分
 (2)方法一:连接OE,ED.
(2)方法一:连接OE,ED.
∵∠BAC=60°,OE=OA,
∴△OAE为等边三角形,
∴∠AOE=60°,
∴∠ADE=30°.
又∵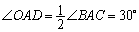 ,
,
∴∠ADE=∠OAD,
∴ED∥AO,············ 6分
∴S△AED=S△OED,
∴阴影部分的面积 = S扇形ODE = 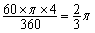 .··············· 9分
.··············· 9分
方法二:同方法一,得ED∥AO,······················ 6分
∴四边形AODE为平行四边形,
∴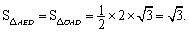 ····················· 7分
····················· 7分
又S扇形ODE-S△OED=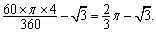 ················· 8分
················· 8分
∴阴影部分的面积 = (S扇形ODE-S△OED) + S△AED =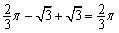 .······ 9分
.······ 9分


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
若函数y=kx-b的图像如图所示,则关于x的不等式k(x-3)-b>0的解集为( )
A. x < 2 B. x > 2 C. x < 5 D. x > 5

查看答案和解析>>
科目:初中数学 来源: 题型:
观察下列关于x的单项式,探究其规律:x,3x2,5x3,7x4,9x5,11x6,….
按 照上述规律,第2015个单项式是
照上述规律,第2015个单项式是
(A) 2015x2015. (B) 4029x2014. (C) 4029x2015. (D) 4031x2015.
查看答案和解析>>
科目:初中数学 来源: 题型:
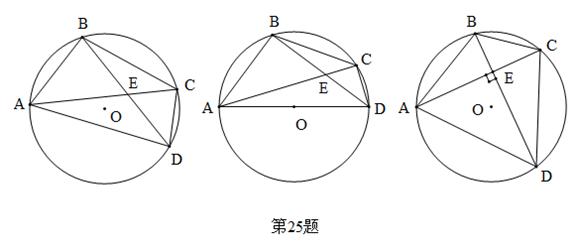
已知:⊙O上两个定点A、B和两个动点C、D,AC与BD交于点E。
(1)如图1,求证: ;
;
(2)如图2,若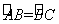 ,AD是⊙O的直径,求证:
,AD是⊙O的直径,求证: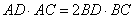 ;
;
(3)如图3,若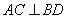 ,点O到AD的距离为2,求BC的长。
,点O到AD的距离为2,求BC的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com