
����Ŀ���Ķ�����IJ��ϣ�������Ķ���գ��ٰ�Ҫ����⣺
��1���Ķ����
sin30��= ![]() ��cos30��=
��cos30��= ![]() ����sin230��+cos230��= ����
����sin230��+cos230��= ����
sin45��= ![]() ��cos45��=
��cos45��= ![]() ����sin245��+cos245��= ����
����sin245��+cos245��= ����
sin60��= ![]() ��cos60��=
��cos60��= ![]() ����sin260��+cos260��= ����
����sin260��+cos260��= ����
��
�۲�������ʽ�����룺���������A������sin2A+cos2A= ����
��2����ͼ�������������ABC�У��������Ǻ����Ķ��弰���ɶ����ԡ�A֤����IJ��룻
��3����֪����AΪ��ǣ�cosA��0����sinA= ![]() ����cosA��
����cosA��
���𰸡�
��1��1��1��1��1
��2��
�⣺��ͼ������B��BD��AC��D�����ADB=90�㣮
��sinA= ![]() ��cosA=
��cosA= ![]() ��
��
��sin2A+cos2A=�� ![]() ��2+��
��2+�� ![]() ��2=
��2= ![]() ��
��
�ߡ�ADB=90�㣬
��BD2+AD2=AB2��
��sin2A+cos2A=1

��3��
�⣺��sinA= ![]() ��sin2A+cos2A=1����AΪ��ǣ�
��sin2A+cos2A=1����AΪ��ǣ�
��cosA= ![]() =
= ![]()
���������⣺��sin30��= ![]() ��cos30��=
��cos30��= ![]() ��
��
��sin230��+cos230��=�� ![]() ��2+��
��2+�� ![]() ��2=
��2= ![]() +
+ ![]() =1����
=1����
��sin45��= ![]() ��cos45��=
��cos45��= ![]() ��
��
��sin245��+cos245��=�� ![]() ��2+��
��2+�� ![]() ��2=
��2= ![]() +
+ ![]() =1����
=1����
��sin60��= ![]() ��cos60��=
��cos60��= ![]() ��
��
��sin260��+cos260��=�� ![]() ��2+��
��2+�� ![]() ��2=
��2= ![]() +
+ ![]() =1����
=1����
�۲�������ʽ�����룺���������A������sin2A+cos2A=1����
�����㾫�������ù��ɶ����ĸ����ͬ�����Ǻ����Ĺ�ϵ��������ƽ�����̣�����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��ֱ֪����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2����������Ǻ���֮��Ĺ�ϵ��ƽ����ϵ��sin2A+cos2A=1����������ϵ��tanAtan(90�㡪A)=1�������й�ϵ��tanA=sinA/cosA ����


 Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д� �����ҵ���������ͯ������ϵ�д�
�����ҵ���������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������Ϊ��1��4����������y=ax2+bx+c��ֱ��y= ![]() x+n���ڵ�A��2��2����ֱ��y=
x+n���ڵ�A��2��2����ֱ��y= ![]() x+n��y�ύ�ڵ�B��x�ύ�ڵ�C
x+n��y�ύ�ڵ�B��x�ύ�ڵ�C
��1����n��ֵ�������ߵĽ���ʽ
��2��PΪ�������ϵĵ㣬��P����ֱ��AB�ĶԳ������x���ϣ����P������
��3����DΪx���Ϸ��������ϵ�һ�㣬��EΪ����һ�㣬��A��B��E��DΪ������ı�Ϊƽ���ı���ʱ��ֱ��д����E�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����C�ǡ�O��һ�㣬����B����O�����ߣ���AC�ӳ��߽��ڵ�D������BC��OE//BC����O�ڵ�E������BE��AC�ڵ�H��
��1����֤��BEƽ�֡�ABC��
��2������OD����BH=BD=2����OD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2014��3��31����ȫ����Сѧ����ȫ�����գ�ijУȫ��ѧ���μ��ˡ��䰮������Ԥ����ˮ��ר����ѧϰ����Ӿ���岻����Ϊ���˽�ѧ���ԡ��岻����֪������������ȡ��200��ѧ�������飬���������������������ͳ��ͼ������⣺ 
��1��������ε����У����ܴ�5���������İٷֱȺ͡����ܴ�3������������
��2������У����2000��ѧ�������Ƹ�У�ܴ�3�������ϣ���3������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������ε�һ��ƽ����x�ᣬһ������y���ϣ����ڵ��⣬���ǵı߳�����Ϊ2��4��6��8����������������A1��A2��A3��A4����ʾ������A1A2��x�ᡢ�ױ�A1A2��A4A5��A4A5��A7A8���������һ����λ����A3�������� �� A92�������� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2013��3��28����ȫ����Сѧ����ȫ�����գ�ijѧУΪ��ǿѧ���İ�ȫ��ʶ����֯��ȫУ1500��ѧ���μӰ�ȫ֪ʶ���������г�ȡ�˲���ѧ���ɼ����÷�ȡ������������Ϊ100�֣�����ͳ�ƣ��������δ��ɵ�Ƶ�ʷֲ�����Ƶ���ֲ�ֱ��ͼ������������⣺ Ƶ�ʷֲ���
������ | Ƶ�� | Ƶ�� |
50.5��60.5 | 16 | 0.08 |
60.5��70.5 | 40 | 0.2 |
70.5��80.5 | 50 | 0.25 |
80.5��90.5 | m | 0.35 |
90.5��100.5 | 24 | n |

��1����γ�ȡ����ѧ���ľ����ɼ�����ͳ�ƣ����У�m= �� n=��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3�����ɼ���70�����£���70�֣���ѧ��Ϊ��ȫ��ʶ��ǿ���д���һ����ǿ��ȫ���������У��ȫ��ʶ��ǿ��ѧ��Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3����1�� ![]() ��1����3��5�����У������ȡһ������Ϊa������aʹ����x�IJ���ʽ��
��1����3��5�����У������ȡһ������Ϊa������aʹ����x�IJ���ʽ�� 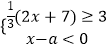 �⣬��ʹ����x�ķ�ʽ����
�⣬��ʹ����x�ķ�ʽ���� ![]() ��
�� ![]() =��1�������⣬��ô��5��������������������a��ֵ֮���ǣ� ��
=��1�������⣬��ô��5��������������������a��ֵ֮���ǣ� ��
A.![]()
B.��2
C.��3
D.�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+c��a��0����x���ཻ��A��B���㣬��y���ཻ�ڵ�C��ֱ��y=kx+n��k��0������B��C���㣬��֪A��1��0����C��0��3������BC=5��
��1���ֱ���ֱ��BC�������ߵĽ���ʽ����ϵʽ����
��2���������ߵĶԳ������Ƿ���ڵ�P��ʹ����B��C��P����Ϊ�������������ֱ�������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����г������п����ľ���װ������AƷ�Ƶ���������ÿ��20Ԫ��BƷ�Ƶ���������ÿ��25Ԫ��С���蹺��A��B����Ʒ�Ƶ��ľ���װ��1000�ף�
��1����С�����蹺��A��B����Ʒ���ľ���װ����22000Ԫ�������������ף�
��2��ƾ��Ա���ڴ������г�������Ʒ���Ի��8���Żݣ���Ա������Ϊ500Ԫ����С�������Ա�����ô˿����蹺��1000���ľ���װ��������yԪ����AƷ���ľ���װ����x���������y��x֮��ĺ�����ϵʽ��
��3����С�������Ա�����ô˿����蹺��1000���ľ���װ��������20000Ԫ�����ƻ���������������������ľ���װ��ÿ���ľ���װС����֧���ʷ�8Ԫ����AƷ��ÿ�����ۼ۸��BƷ����5Ԫ������������㣬AƷ�Ƶ��ľ���װÿ���۲����ڶ���Ԫʱ�Ų�������������ȡ��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com