
分析 (1)利用二次根式的乘除法法则求解即可;
(2)利用二次根式的乘除法法则求解即可;
(3)利用二次根式的乘除法法则求解即可.
解答 解:(1)$\sqrt{2\frac{1}{2}}$÷3$\sqrt{28}$×(-5$\sqrt{2\frac{2}{7}}$)
=$\frac{\sqrt{10}}{2}$×$\frac{1}{6\sqrt{7}}$×(-$\frac{20\sqrt{7}}{7}$)
=-$\frac{5\sqrt{10}}{21}$;
(2)5x$\sqrt{xy}$÷3$\sqrt{\frac{y}{x}}$×$\frac{1}{3}$$\sqrt{\frac{x}{y}}$
=5x$\sqrt{xy}$÷$\frac{3\sqrt{xy}}{x}$×$\frac{\sqrt{xy}}{3y}$
=5x$\sqrt{xy}$×$\frac{x}{3\sqrt{xy}}$×$\frac{\sqrt{xy}}{3y}$
=$\frac{5{x}^{2}\sqrt{xy}}{9y}$;
(3)$\frac{2}{b}$$\sqrt{ab}$5•(-$\frac{3}{2}$$\sqrt{{a}^{3}b}$)÷3$\sqrt{\frac{b}{a}}$
=2b2$\sqrt{ab}$•(-$\frac{3}{2}$a$\sqrt{ab}$)•$\frac{a}{3\sqrt{ab}}$
=-3a2b2$\sqrt{ab}$.
点评 本题主要考查了二次根式的乘除法,解题的关键是熟记二次根式的乘除法法则.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 有两边相等的平行四边形是菱形 | B. | 对角线垂直的四边形是菱形 | ||
| C. | 四个角相等的菱形是正方形 | D. | 两条对角线相等的四边形是矩形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 市盈率是某种股票每股市价与每股盈利的比率(即:某股票的市盈率=该股票当前每股市价÷该股票上一年每股盈利),市盈利估计股票价值的最基本的指标之一,一般认为该比率保持在30以下的是正常的,风险小,值得购买;过大则说明股价高,风险大,购买时应谨慎.某日王先生通过互联网了解到如下三方面的信息:
市盈率是某种股票每股市价与每股盈利的比率(即:某股票的市盈率=该股票当前每股市价÷该股票上一年每股盈利),市盈利估计股票价值的最基本的指标之一,一般认为该比率保持在30以下的是正常的,风险小,值得购买;过大则说明股价高,风险大,购买时应谨慎.某日王先生通过互联网了解到如下三方面的信息:| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 市盈率 | 25 | 800 | 61 | 19 | 18 | 28 | 28 | 35 | 59 | 80 | 62 | 80 | 80 | 82 | 43 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
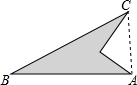 一个零件的形状如图所示,按规定∠BAC应为直角,工人师傅测得∠ADC=90°,AD=6,CD=8,AB=24,BC=26,请你帮他看一下,这个零件符合要求吗?为什么.
一个零件的形状如图所示,按规定∠BAC应为直角,工人师傅测得∠ADC=90°,AD=6,CD=8,AB=24,BC=26,请你帮他看一下,这个零件符合要求吗?为什么.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
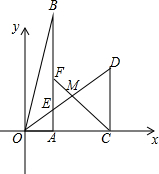 如图,在直角坐标系xOy中,Rt△OAB和Rt△OCD的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,Rt△OAB的面积恒为$\frac{1}{2}$.
如图,在直角坐标系xOy中,Rt△OAB和Rt△OCD的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,Rt△OAB的面积恒为$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com