
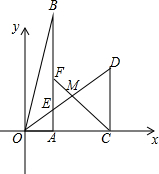
 ��ͼ����ֱ������ϵxOy�У�Rt��OAB��Rt��OCD��ֱ�Ƕ���A��Cʼ����x����������ϣ�B��D�ڵ�һ�����ڣ���B��ֱ��OD�Ϸ���OC=CD��OD=2��MΪOD���е㣬AB��OD�ཻ��E������Bλ�ñ仯ʱ��Rt��OAB�������Ϊ$\frac{1}{2}$��
��ͼ����ֱ������ϵxOy�У�Rt��OAB��Rt��OCD��ֱ�Ƕ���A��Cʼ����x����������ϣ�B��D�ڵ�һ�����ڣ���B��ֱ��OD�Ϸ���OC=CD��OD=2��MΪOD���е㣬AB��OD�ཻ��E������Bλ�ñ仯ʱ��Rt��OAB�������Ϊ$\frac{1}{2}$������ ��1�����ݵ���ֱ�������ε����ʵó�CD=OC=$\sqrt{2}$���ó���D�����ꣻ
��2������ֱ�������ε������ʽ���н��
��3���֡�EBD=90��ʱ�͡�EBD=45������������з���������ֱ�����κ����ε��ж����
��� �⣺��1����RT��OCD�У�OC=CD��OD=2��
��CD=OC=$\sqrt{2}$��
���D�����꣨$\sqrt{2}$��$\sqrt{2}$����
��2����RT��OAB�����Ϊ$\frac{1}{2}$����B��t��$\frac{1}{t}$����
��BD2=AC2+��AB-CD��2��
��$B{D}^{2}=��t-\sqrt{2}��^{2}+��\frac{1}{t}-\sqrt{2}��^{2}$
=${t}^{2}+\frac{1}{{t}^{2}}-2\sqrt{2}��t+\frac{1}{t}��+4$
=$��t+\frac{1}{t}��^{2}-2\sqrt{2}��t+\frac{1}{t}��+2$
=$��t+\frac{1}{t}-\sqrt{2}��^{2}$��
��$BD=|t+\frac{1}{t}-\sqrt{2}|=t+\frac{1}{t}-\sqrt{2}$��
��3�������BDEΪֱ�������Σ���Ϊ��BED=45�㣬
�ٵ���EBD=90��ʱ����ʱF��E��M�����غϣ���ͼ1��ʾ��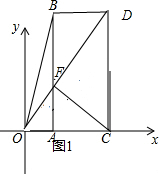
��ΪBF��x�ᣬDC��x�ᣬ����BF��DC�����Դ�ʱ�ı���BDCFΪֱ�����Σ�
�ڵ���EBD=45��ʱ����ͼ2��ʾ��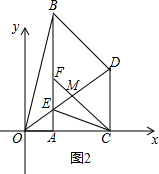
��ΪCF��OD������BD��CF����BF��x�ᣬDC��x�ᣬ����BF��DC�����Դ�ʱ�ı���BDCF��ƽ���ı��Σ�����OB���ڡ�BOD�У�OB2=OD2+BD2��
${t}^{2}+\frac{1}{{t}^{2}}=4+��t+\frac{1}{t}-\sqrt{2}��^{2}$����$t+\frac{1}{t}=2\sqrt{2}$��$DB=t+\frac{1}{t}-\sqrt{2}=2\sqrt{2}-\sqrt{2}=\sqrt{2}$��
��ʱBD=CD=$\sqrt{2}$�����Դ�ʱ�ı���BDCFΪ���Σ�
���� ���⿼��һ�κ������ۺ��⣬�ؼ��Ǹ��ݵ���ֱ�������ε����ʵó�CD=OC=$\sqrt{2}$����ע��֡�EBD=90��ʱ�͡�EBD=45������������з�����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x-3��2=16 | B�� | ��x+3��2=2 | C�� | ��x-6��2=29 | D�� | ��x-3��2=2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
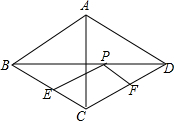 ��ͼ����֪����ABCD�У��Խ���AC=12��BD=16����E��F�ֱ�Ϊ��BC��CD���е㣬��P�Խ���BD��һ���㣬��PE+PF����СֵΪ��������
��ͼ����֪����ABCD�У��Խ���AC=12��BD=16����E��F�ֱ�Ϊ��BC��CD���е㣬��P�Խ���BD��һ���㣬��PE+PF����СֵΪ��������| A�� | 10 | B�� | 12 | C�� | 14 | D�� | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���ߣ�x/cm�� | ������Ƶ���� |
| 145��x��155 | 10 |
| 155��x��165 | 25 |
| 165��x��175 | a |
| 175��x��185 | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
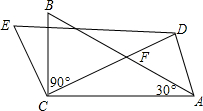 ��ͼ��ʾ���ڡ�ABC�У���ACB=90�㣬��A=30�㣬����ABC�Ƶ�C����ʱ����ת����0�㣼����90�㣩�á�DEC����CD��AB�ڵ�F������ACD=40���20��ʱ����ADFΪ���������Σ�
��ͼ��ʾ���ڡ�ABC�У���ACB=90�㣬��A=30�㣬����ABC�Ƶ�C����ʱ����ת����0�㣼����90�㣩�á�DEC����CD��AB�ڵ�F������ACD=40���20��ʱ����ADFΪ���������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com