
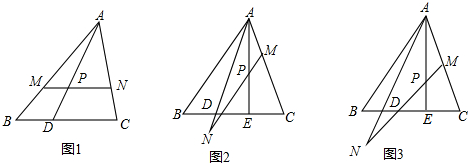
分析 (1)由MN∥BC可得△AMP∽△ABD,△APN∽△ADC,然后运用相似三角形的性质即可得到$\frac{PM}{DB}$=$\frac{AP}{AD}$=$\frac{PN}{DC}$,再由CD=2BD可得PN=2PM;
(2)借鉴(1)中的经验,可通过添加辅助线,构造(1)中的双A型相似模型(过点C作CF∥MN,交AN的延长线于F,交AE的延长线于G,如图2),易得$\frac{PN}{GF}$=$\frac{AP}{AG}$=$\frac{PM}{GC}$,要证PN=3PM,只需证FG=3GC,即证FC=4GC.由AB∥FC可得△ABD∽△FCD,从而得到$\frac{AB}{FC}$=$\frac{BD}{CD}$,再由点D是BC的三等分点可得$\frac{AB}{FC}$=$\frac{1}{2}$,同理可得$\frac{AB}{GC}$=2,问题得以解决;
(3)借鉴(2)中的经验,过点C作CF∥MN,交AN的延长线于F,交AE的延长线于G,如图3.由CF∥MN可证到$\frac{PN}{GF}$=$\frac{AP}{AG}$=$\frac{PM}{GC}$,再由PN=5PM可得GF=5GC,即FC=6GC.由AB∥MN,CF∥MN可得AB∥FC,从而可证到$\frac{AB}{FC}$=$\frac{BD}{DC}$,$\frac{AB}{GC}$=$\frac{BE}{EC}$,根据合比定理可得$\frac{AB}{AB+6GC}$=$\frac{BD}{BC}$,$\frac{AB+GC}{GC}$=$\frac{BC}{EC}$,再由BD=CE可得$\frac{AB}{AB+6GC}$•$\frac{AB+GC}{GC}$=1,整理得AB2=6GC2,即AB=$\sqrt{6}$GC,从而可得BE=$\sqrt{6}$EC,即可得到DE与EC、BC与EC的关系,就可解决问题.
解答 证明:(1)如图1,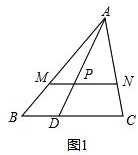
∵MN∥BC,
∴△AMP∽△ABD,△APN∽△ADC,
∴$\frac{AP}{AD}$=$\frac{PM}{DB}$,$\frac{AP}{AD}$=$\frac{PN}{DC}$,
∴$\frac{PM}{DB}$=$\frac{PN}{DC}$.
∵CD=2BD,
∴PN=2PM;
(2)PN=3PM.
理由:过点C作CF∥MN,交AN的延长线于F,交AE的延长线于G,如图2.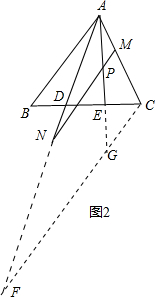
∵MN∥AB,∴AB∥FC,
∴△ABD∽△FCD,
∴$\frac{AB}{FC}$=$\frac{BD}{CD}$.
∵点D是BC的三等分点,
∴$\frac{BD}{CD}$=$\frac{1}{2}$,
∴$\frac{AB}{FC}$=$\frac{1}{2}$.
同理可得$\frac{AB}{GC}$=$\frac{BE}{EC}$=2,
∴FC=2AB=4GC,
∴FG=3GC.
∵MN∥FC,
∴△ANP∽△AFG,△AMP∽△ACG,
∴$\frac{PN}{GF}$=$\frac{AP}{AG}$=$\frac{PM}{GC}$,
∴PN=3PM;
(3)答案为$\frac{7-2\sqrt{6}}{5}$.
提示:过点C作CF∥MN,交AN的延长线于F,交AE的延长线于G,如图3.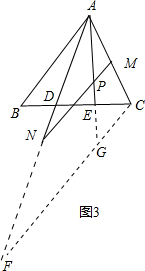
由CF∥MN可证到$\frac{PN}{GF}$=$\frac{AP}{AG}$=$\frac{PM}{GC}$,再由PN=5PM可得GF=5GC,即FC=6GC.
由AB∥MN,CF∥MN可得AB∥FC,从而可证到$\frac{AB}{FC}$=$\frac{BD}{DC}$,$\frac{AB}{GC}$=$\frac{BE}{EC}$,
则有$\frac{AB}{AB+6GC}$=$\frac{BD}{BC}$,$\frac{AB+GC}{GC}$=$\frac{BC}{EC}$.
∵BD=CE,∴$\frac{AB}{AB+6GC}$•$\frac{AB+GC}{GC}$=1,
整理得AB2=6GC2,
∴AB=$\sqrt{6}$GC.
∴$\frac{BE}{EC}$=$\frac{AB}{GC}$=$\sqrt{6}$,即BE=$\sqrt{6}$EC,
∴DE=BE-BD=$\sqrt{6}$EC-EC=($\sqrt{6}$-1)EC.
∵BC=BE+EC=$\sqrt{6}$EC+EC=($\sqrt{6}$+1)EC,
∴$\frac{DE}{BC}$=$\frac{\sqrt{6}-1}{\sqrt{6}+1}$=$\frac{7-2\sqrt{6}}{5}$.
点评 本题主要考查了相似三角形的判定与性质、合比定理等知识,利用(1)中的图形及有关结论是解决第(2)、(3)两小题的关键,是一道好题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
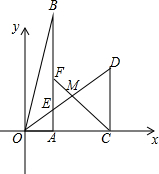 如图,在直角坐标系xOy中,Rt△OAB和Rt△OCD的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,Rt△OAB的面积恒为$\frac{1}{2}$.
如图,在直角坐标系xOy中,Rt△OAB和Rt△OCD的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,Rt△OAB的面积恒为$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
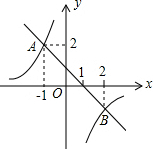 如图,直线y=-x+b与双曲线y=$\frac{k}{x}$交于点A,B,则不等式组$\frac{k}{x}$<-x+b<0的解集为( )
如图,直线y=-x+b与双曲线y=$\frac{k}{x}$交于点A,B,则不等式组$\frac{k}{x}$<-x+b<0的解集为( )| A. | 0<x<2 | B. | x<-1或0<x<2 | C. | -1<x<2 | D. | 1<x<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com