
【题目】规定两数![]() 、
、![]() 之间的一种运算,记作(
之间的一种运算,记作(![]() ,
,![]() );如果
);如果![]() ,那么(
,那么(![]() ,
,![]() )=c.
)=c.
例如:因为![]() ,所以(2,8)=3.
,所以(2,8)=3.
(1)根据上述规定,填空:(4,16)=_________,(7,1)=___________,(_______,![]() )=-2.
)=-2.
(2)小明在研究这种运算时发现一个现象:(![]() ,
,![]() )=(3,4)小明给出了如下的证明:
)=(3,4)小明给出了如下的证明:
设(![]() ,
,![]() )=
)=![]() ,则
,则![]() ,即
,即![]()
所以![]() ,即(3,4)=
,即(3,4)=![]() ,
,
所以(![]() ,
,![]() )=(3,4).
)=(3,4).
请你尝试运用这种方法解决下列问题:
①证明:(6,45)-(6,9)=(6,5)
②猜想:(![]() ,
,![]() )+(
)+(![]() ,
,![]() )=(____________,____________),(结果化成最简形式).
)=(____________,____________),(结果化成最简形式).
【答案】(1)2,0,5;
(2)①证明见解析;②(x+1),(y2-3y+2).
【解析】
(1)根据规定的两数之间的运算法则解答;
(2)①根据同底数幂的乘法法则,结合定义证明;②根据例题和①中证明的式子作为公式进行变形即可.
(1)因为42=16,所以【4,16】=2.
因为70=1,所以【7,1】=0.
因为5-2=![]() ,所以【5,
,所以【5,![]() 】=-2.
】=-2.
故答案为:2,0,5;
(2)①证明:设【6,9】=x,【6,5】=y,则6x=9,6y=5,
∴5×9=45=6x6y=6x+y,
∴【6,45】=x+y,
则:【6,45】=【6,9】+【6,5】,
∴【6,45】-【6,9】=【6,5】;
②∵【3n,4n】=【3,4】,
∴【(x+1)m,(y-1)m】=【(x+1),(y-1)】,【(x+1)n,(y-2)n】=【(x+1),(y-2)】,
∴【(x+1)m,(y-1)m】+【(x+1)n,(y-2)n】,
=【(x+1),(y-1)】+【(x+1),(y-2)】,
=【(x+1),(y-1)(y-2)】,
=【(x+1),(y2-3y+2)】.
故答案为:(x+1),(y2-3y+2).


科目:初中数学 来源: 题型:
【题目】学校为了让同学们走向操场、积极参加体育锻炼,启动了“学生阳光体育运动”,张明和李亮在体育运动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
平均数 | 中位数 | 方差 | |
张明 | 13.3 | 0.004 | |
李亮 | 13.3 | 0.02 |
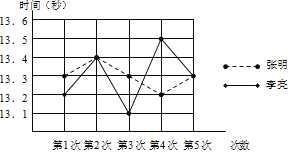
(1)张明第2次的成绩为: 秒;
(2)张明成绩的平均数为: ;李亮成绩的中位数为: ;
(3)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为准备母亲节礼物,同学们委托小明用其支付宝余额团购鲜花或礼盒.每束鲜花的售价相同,每份礼盒的售价也相同.若团购15束鲜花和18份礼盒,余额差80元;若团购18束鲜花和15份礼盒,余额剩70元.若团购19束鲜花和14份礼盒,则支付宝余额剩_______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点A,B,C,D在一条直线上,填写下列空格:
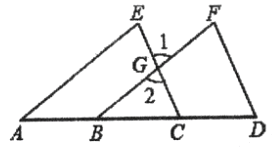
∵AE∥BF(已知)
∴∠E=∠1(______________________)
∵∠E=∠F(已知〉
∴∠_____=∠F(________________)
∴________∥_________(________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成相应学习任务:
四点共圆的条件
我们知道,过任意一个三角形的三个顶点能作一个圆,过任意一个四边形的四个顶点能作一个圆吗?小明经过实践探究发现:过对角互补的四边形的四个顶点能作一个圆,下面是小明运用反证法证明上述命题的过程:
已知:在四边形ABCD中,∠B+∠D=180°.
求证:过点A、B、C、D可作一个圆.
证明:如图(1),假设过点A、B、C、D四点不能作一个圆,过A、B、C三点作圆,若点D在圆外,设AD与圆相交于点E,连接CE,则∠B+∠AEC=180°,而已知∠B+∠D=180°,所以∠AEC=∠D,而∠AEC是△CED的外角,∠AEC>∠D,出现矛盾,故假设不成立,因此点D在过A、B、C三点的圆上.
如图(2)假设过点A、B、C、D四点不能作一个圆,过A、B、C三点作圆,若点D在圆内,设AD的延长线与圆相交于点E,连接CE,则∠B+∠AEC=180°,而已知∠B+∠ADC=180°,所以∠AEC=∠ADC,而∠ADC是△CED的外角,∠ADC>∠AEC,出现矛盾,故假设不成立,因此点D在过A、B、C三点的圆上.
因此得到四点共圆的条件:过对角互补的四边形的四个顶点能作一个圆.
学习任务:
(1)材料中划线部分结论的依据是 .
(2)证明过程中主要体现了下列哪种数学思想: (填字母代号即可)
A、函数思想 B、方程思想 C、数形结合思想 D、分类讨论思想
(3)如图(3),在四边形ABCD中,∠ABC=∠ADC=90°,∠CAD=16°.AD=BD,则求∠ADB的大小.
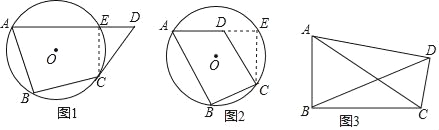
查看答案和解析>>
科目:初中数学 来源: 题型:
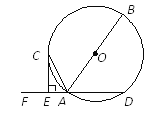
【题目】如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线上的一点,过⊙O上一点C作⊙O的切线交DF于点E,CE⊥DF.
(1)求证:AC平分∠FAB;
(2)若AE=1,CE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
某商店经销《超能陆战队》超萌“小白”(图1)玩具,“小白”玩具每个进价60元.为进行促销,商店制定如下“优惠”方案:如果一次销售数量不超过10个,则销售单价为100元/个;如果一次销售数量超过10个,每增加一个,所有“小白”玩具销售单价降低1元/个,但单价不得低于80元/个.一次销售“小白”玩具的单价y(元/个)与销售数量x(个)之间的函数关系如图2所示.

(1)求m的值并解释射线BC所表示的实际意义;
(2)写出该店当一次销售x个时,所获利润w(元)与x(个)之间的函数关系式;
(3)店长经过一段时间的销售发现:即并不是销量越大利润越大(比如,卖25个赚的钱反而比卖30个赚的钱多).为了不出现这种现象,在其他条件不变的情况下,店长应把原来的最低单价80(元/个)至少提高到多少元/个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A∶P′C=1∶3,则P′A∶PB=( )

A. 1∶![]() B. 1∶2 C.
B. 1∶2 C. ![]() ∶2 D. 1∶
∶2 D. 1∶![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com