
【题目】若点P在x轴上,点A(1,1),O是坐标原点,且△AOP是等腰三角形,则点P的坐标是________.
【答案】(2, 0),(![]() ,0),(1,0)或(-
,0),(1,0)或(-![]() ,0);
,0);
【解析】
此题没有说明是那两条边为腰长,所以要分类讨论从而求解.
解:(1)当点P在x轴正半轴上,
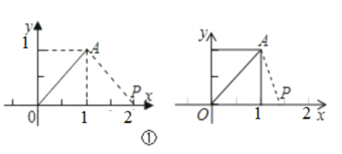
以OA为腰时,
∵A的坐标是(1,1),
∵∠AOP= 45°,OA= ![]() ,
,
∴P的坐标是(2, 0)或(![]() ,0);
,0);
以OA为底边时,
∵点A的坐标是(1,1),
∴当点P的坐标为:(1,0)时,OP= AP;
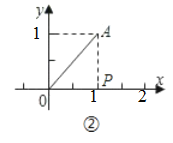
(2)当点P在x轴负半轴上,
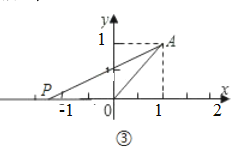
以OA为腰时,
∵A的坐标是(1,1),
∴OA=![]() ,
,
∴OA= OP=![]() ,
,
∴P的坐标是(-![]() ,0),
,0),
综上:P的坐标是(2, 0),(![]() ,0),(1,0)或(-
,0),(1,0)或(-![]() ,0);
,0);
故答案为:(2, 0),(![]() ,0),(1,0)或(-
,0),(1,0)或(-![]() ,0);
,0);


科目:初中数学 来源: 题型:
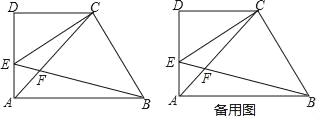
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮与小明做投骰子(质地均匀的正方体)的实验与游戏.
(1)在实验中他们共做了50次试验,试验结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 10 | 9 | 6 | 9 | 8 | 8 |
填空:此次实验中,“1点朝上”的频率是 ;
② 小亮说:“根据试验,出现1点朝上的概率最大.”他的说法正确吗?为什么?
(2)小明也做了大量的同一试验,并统计了“1点朝上”的次数,获得的数据如下表:
试验总次数 | 100 | 200 | 500 | 1000 | 2000 | 5000 | 10000 |
1点朝上的次数 | 18 | 34 | 82 | 168 | 330 | 835 | 1660 |
1点朝上的频率 | 0.180 | 0.170 | 0.164 | 0.168 | 0.165 | 0.167 | 0.166 |
“1点朝上”的概率的估计值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B,C三点在同一条数轴上.
(1)、若点A,B表示的数分别为-4,2,且BC=![]() AB,则点C表示的数是 ;
AB,则点C表示的数是 ;
(2)、点A,B表示的数分别为m,n,且m<n.
①若AC-AB=2,求点C表示的数(用含m,n的式子表示);
②点D是这条数轴上的一个动点,且点D在点A的右侧(不与点B重合),当AD=2AC,BC=![]() BD,求线段AD的长(用含m,n的式子表示).
BD,求线段AD的长(用含m,n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小李8时骑自行车从家里出发,到野外郊游,16时回到家里.他离家的距离s(千米)与时间t(时)之间的函数关系可以用图中的折线表示.现有如下信息:
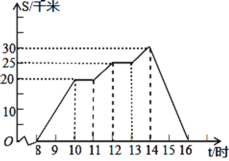
(1)小李到达离家最远的地方的时间是14时;
(2)小李第一次休息时间是10时;
(3)11时到12时,小李骑了5千米;
(4)返回时,小李的平均车速是10千米/时.
其中,正确的信息有___________________(填番号).
查看答案和解析>>
科目:初中数学 来源: 题型:
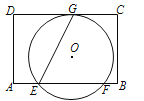
【题目】如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE=![]() AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=
AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=![]() .当边AD或BC所在的直线与⊙O相切时,AB的长是 .
.当边AD或BC所在的直线与⊙O相切时,AB的长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=1,DE=3,∠EFB′=60°,则矩形ABCD的面积是( )
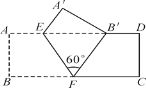
A.4B.8C.3![]() D.4
D.4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车租赁公司准备购买A,B两种型号的新能源汽车10辆.汽车厂商提供了如下两种购买方案:
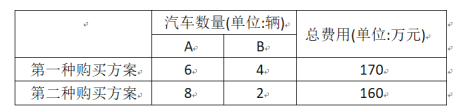
(1)A,B两种型号的新能源汽车每辆的价格各是多少万元?
(2)为了支持新能源汽车产业的发展,国家对新能源汽车发放一定的补贴.已知国家对A, B两种型号的新能源汽车补贴资金分别为每辆3万元和4万元.通过测算,该汽车租赁公司在此次购车过程中,可以获得国家补贴资金不少于34万元,公司需要支付资金不超过145万元,请你通过计算求出有几种购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com