
����Ŀ��ij��������˾������A,B�����ͺŵ�����Դ����10��.���������ṩ���������ֹ���:
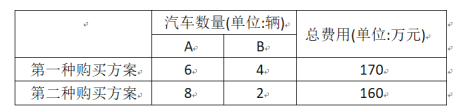
(1)A,B�����ͺŵ�����Դ����ÿ���ļ۸���Ƕ�����Ԫ?
(2)Ϊ��֧������Դ������ҵ�ķ�չ�����Ҷ�����Դ��������һ���IJ���.��֪���Ҷ�A, B�����ͺŵ�����Դ���������ʽ�ֱ�Ϊÿ��3��Ԫ��4��Ԫ.ͨ�����㣬����������˾�ڴ˴ι��������У����Ի�ù��Ҳ����ʽ�����34��Ԫ����˾��Ҫ֧���ʽ���145��Ԫ������ͨ����������м��ֹ���.
���𰸡���1����A�ͺŵ�����Դ����ÿ���۸�15��Ԫ��B�ͺŵ�����Դ����ÿ���۸�20��Ԫ����2�������ֹ���.
��������
��1���ֱ���A��B�ͺŵ�����Դ����ÿ���ļ۸�Ϊx��y��Ԫ�����ݱ�����г�һ����Ԫһ�η����飬��˷����鼴�ɵó��𰸣�
��2���蹺��A�ͳ�a��������B�ͳ�(10-a)��������������г�һ��һԪһ�β���ʽ�飬��˲���ʽ�飬ȡ�������⣬���ɵó���.
�⣺��1����A�ͺŵ�����Դ����ÿ���۸�x��Ԫ��B�ͺŵ�����Դ����ÿ���۸�y��Ԫ.
������ɵã�![]()
��ã�![]()
��A�ͺŵ�����Դ����ÿ���۸�15��Ԫ��B�ͺŵ�����Դ����ÿ���۸�20��Ԫ.
��2���蹺��A�ͳ�a��������B�ͳ�(10-a)��.
������ɵ�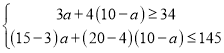
��ã�![]()
��a��ȡֵΪ4��5��6.
��������ֹ���.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P��x���ϣ���A��1,1����O������ԭ�㣬�ҡ�AOP�ǵ��������Σ����P��������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ͬ�ͺŵ��ֻ�(�ֱ��ΪA��B)����֮ƥ���2��������(�ֱ��Ϊa��b)ɢ�ҵط��������ϣ�
(1)�����ֻ������ȡһ�����ٴӱ����������ȡһ������ǡ��ƥ��ĸ��ʣ�
(2)�����ֻ��ͱ����������ȡ�������û���״ͼ�����б�����ǡ��ƥ��ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=2x+n��x�ᡢy��ֱ��ڵ�A��B����˫����![]() �ڵ�һ�����ڽ��ڵ�C��1��m����ֱ��CQ�Ľ���ʽΪ��y=kx+b(k��0)
�ڵ�һ�����ڽ��ڵ�C��1��m����ֱ��CQ�Ľ���ʽΪ��y=kx+b(k��0)

��1����m��n��ֵ��
��2����x���ϵĵ�D��3��0����ƽ����y���ֱ��l���ֱ���ֱ��AB��˫����![]() ���ڵ�P��Q�����APQ�������
���ڵ�P��Q�����APQ�������
��3��ֱ��д��![]() �Ľ⼯
�Ľ⼯
��4��ֱ��д��ֱ����![]() �Ľ⡣
�Ľ⡣
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У�
����Ϊ![]() ���߶�
���߶�![]() ��ijһ����ƽ��
��ijһ����ƽ��![]() ��ƽ�ƺ��߶�
��ƽ�ƺ��߶�![]() �ij�Ϊ
�ij�Ϊ![]() ��
��
�������εĸ����������ڲ���
�������ε��ڽǺ�����Ǻ͵�������
��ƽ����ͬһֱ�ߵ���ֱ��ƽ�У�
�������ǵ����߷ֱ�ƽ�У�������������ȣ�����������У� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУΪ����ͬѧ������ٳ��������μ����������������ˡ�ѧ�����������˶����������������������˶��б����μ��˰���ѵ��С�飮�ڽ����ΰ���ѵ���У��������������˵IJ��Գɼ�������ͳ�ƺͷ����������ͼ���е���Ϣ����������⣺
ƽ���� | ��λ�� | ���� | |
���� | 13.3 | 0.004 | |
���� | 13.3 | 0.02 |
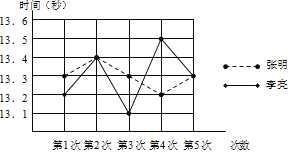
��1��������2�εijɼ�Ϊ�����������룻
��2�������ɼ���ƽ����Ϊ�����������������ɼ�����λ��Ϊ������������
��3�����ڴ�������������ѡ��һ���ɼ������ȥ�μӱ��������������ǵĽ�����Ӧ��ѡ��˭����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1������5������+3��+����9��������7��
��2����+5![]() ��+����3
��+����3![]() ��+����6
��+����6![]() ��+����15
��+����15![]() ��
��
��3��|��6![]() |+����8��+|��3��
|+����8��+|��3��![]() |
|
��4��78������![]() ��+����11��������
��+����11��������![]() ��+����33����0.6
��+����33����0.6
��5������2��2010������0.5��2009+����6![]() ����7
����7
��6����14��![]() ��[2������3����2]
��[2������3����2]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ������Ϊ4Ԫ������Ʒ������ÿ��5Ԫ�ļ۸����ۣ�ÿ��������300��������ÿ��6Ԫ�ļ۸����ۣ�ÿ��������200�����ٶ�ÿ�����ۼ���![]() ��������۸�
��������۸�![]() ��Ԫ/����֮������һ�κ�����ϵ��
��Ԫ/����֮������һ�κ�����ϵ��
��1��������![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2���������ۼ۸�Ϊ����ʱ������ʹÿ�µ��������ÿ�µ���������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ������Ӧѧϰ����
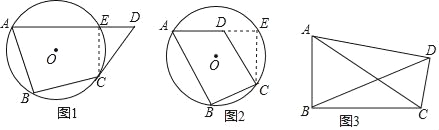
�ĵ㹲Բ������
����֪����������һ�������ε�������������һ��Բ��������һ���ı��ε��ĸ���������һ��Բ��С������ʵ��̽�����֣����Խǻ������ı��ε��ĸ���������һ��Բ��������С�����÷�֤��֤����������Ĺ��̣�
��֪�����ı���ABCD�У���B+��D=180�㣮
��֤������A��B��C��D����һ��Բ��
֤������ͼ��1�����������A��B��C��D�ĵ㲻����һ��Բ����A��B��C������Բ������D��Բ�⣬��AD��Բ�ཻ�ڵ�E������CE������B+��AEC=180��������֪��B+��D=180�㣬������AEC=��D������AEC����CED����ǣ���AEC����D������ì�ܣ��ʼ��費��������˵�D�ڹ�A��B��C�����Բ�ϣ�
��ͼ��2���������A��B��C��D�ĵ㲻����һ��Բ����A��B��C������Բ������D��Բ�ڣ���AD���ӳ�����Բ�ཻ�ڵ�E������CE������B+��AEC=180��������֪��B+��ADC=180�㣬������AEC=��ADC������ADC����CED����ǣ���ADC����AEC������ì�ܣ��ʼ��費��������˵�D�ڹ�A��B��C�����Բ�ϣ�
��˵õ��ĵ㹲Բ�����������Խǻ������ı��ε��ĸ���������һ��Բ��
ѧϰ����
��1�������л��߲��ֽ��۵��������� ����
��2��֤����������Ҫ����������������ѧ˼�룺�� ��������ĸ���ż��ɣ�
A������˼�� B������˼�� C�����ν��˼�� D����������˼��
��3����ͼ��3�������ı���ABCD�У���ABC=��ADC=90�㣬��CAD=16�㣮AD=BD��������ADB�Ĵ�С��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com