
【题目】计算:
(1)(﹣5)﹣(+3)+(﹣9)﹣(﹣7)
(2)(+5![]() )+(﹣3
)+(﹣3![]() )+(﹣6
)+(﹣6![]() )+(﹣15
)+(﹣15![]() )
)
(3)|﹣6![]() |+(﹣8)+|﹣3﹣
|+(﹣8)+|﹣3﹣![]() |
|
(4)78×(﹣![]() )+(﹣11)×(﹣
)+(﹣11)×(﹣![]() )+(﹣33)×0.6
)+(﹣33)×0.6
(5)(﹣2)2010×(﹣0.5)2009+(﹣6![]() )×7
)×7
(6)﹣14﹣![]() ×[2﹣(﹣3)﹣2]
×[2﹣(﹣3)﹣2]
【答案】(1)-10;(2)﹣19![]() ;(3)﹣
;(3)﹣![]() ;(4)﹣60;(5)﹣50
;(4)﹣60;(5)﹣50![]() ;(6)
;(6)![]()
【解析】
(1)先同号相加,再异号相加即可求解;
(2)先算同分母分数,再相加即可求解;
(3)先算绝对值,再算同分母分数,再相加即可求解;
(4)根据乘法分配律简便计算;
(5)根据积的乘方简便计算;
(6)先算乘方,再算乘法,最后算减法;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
(1)(﹣5)﹣(+3)+(﹣9)﹣(﹣7)
=(﹣5)+(﹣3)+(﹣9)﹣(﹣7)
=﹣(5+3+9)+7
=﹣10;
(2)(+5![]() )+(﹣3
)+(﹣3![]() )+(﹣6
)+(﹣6![]() )+(﹣15
)+(﹣15![]() )
)
=(+5![]() ﹣6
﹣6![]() )+[(﹣3
)+[(﹣3![]() )+(﹣15
)+(﹣15![]() )]
)]
=﹣![]() +(﹣19)
+(﹣19)
=﹣19![]() ;
;
(3)|﹣6![]() |+(﹣8)+|﹣3﹣
|+(﹣8)+|﹣3﹣![]() |
|
=6![]() ﹣2
﹣2![]() +(﹣8)+3
+(﹣8)+3![]()
=6![]() +(﹣2
+(﹣2![]() +3
+3![]() )+(﹣8)
)+(﹣8)
=6![]() +1+(﹣8)
+1+(﹣8)
=6![]() ﹣7
﹣7
=﹣![]() ;
;
(4)78×(﹣![]() )+(﹣11)×(﹣
)+(﹣11)×(﹣![]() )+(﹣33)×0.6
)+(﹣33)×0.6
=78×(﹣![]() )+(﹣11)×(﹣
)+(﹣11)×(﹣![]() )+(﹣33)×
)+(﹣33)×![]()
=![]() ×(﹣78+11﹣33)
×(﹣78+11﹣33)
=![]() ×(﹣100)
×(﹣100)
=﹣60;
(5)(﹣2)2010×(﹣0.5)2009+(﹣6![]() )×7
)×7
=[(﹣2)×(﹣0.5)]2009×(﹣2)+(﹣![]() )×7
)×7
=﹣2﹣![]()
=﹣50![]() ;
;
(6)﹣14﹣![]() ×[2﹣(﹣3)﹣2]
×[2﹣(﹣3)﹣2]
=﹣1﹣![]() ×[2﹣9]
×[2﹣9]
=﹣1﹣![]() ×(﹣7)
×(﹣7)
=﹣1+![]()
=![]() .
.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
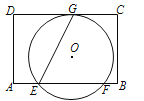
【题目】如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE=![]() AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=
AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=![]() .当边AD或BC所在的直线与⊙O相切时,AB的长是 .
.当边AD或BC所在的直线与⊙O相切时,AB的长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习了“求简单随机事件发生的可能性大小”知识后,小敏,小聪,小丽三人分别编写了一道有关随机事件的试题并进行了解答.小敏,小聪,小丽编写的试题分别是下面的(1)(2)(3).
(1)一个不透明的盒子里装有4个红球,2个白球,除颜色外其它都相同,搅均后,从中随意摸出一个球,摸出红球的可能性是多少?解:P(摸出一个红球)=![]() .
.
(2)口袋里装有如图所示的1角硬币2枚、5角硬币2枚、1 元硬币1枚.搅均后,从中随意摸出一枚硬币,摸出1角硬币的可能性是多少?解:P(摸出1角的硬币)=![]() .
.
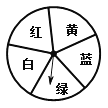
(3)如图,是一个转盘,盘面上有5个全等的扇形区域,每个区域显示有不同的颜色,轻轻转动转盘,当转盘停止后,指针对准红色区域的可能性是多少?解:P(指针对准红色区域)=![]() .
.
问题:根据以上材料回答问题:小敏,小聪,小丽三人中,谁编写的试题及解答是正确的,并简要说明其他两人所编试题或解答的不足之处.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车租赁公司准备购买A,B两种型号的新能源汽车10辆.汽车厂商提供了如下两种购买方案:
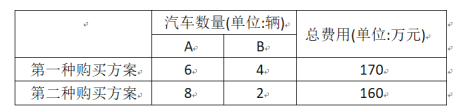
(1)A,B两种型号的新能源汽车每辆的价格各是多少万元?
(2)为了支持新能源汽车产业的发展,国家对新能源汽车发放一定的补贴.已知国家对A, B两种型号的新能源汽车补贴资金分别为每辆3万元和4万元.通过测算,该汽车租赁公司在此次购车过程中,可以获得国家补贴资金不少于34万元,公司需要支付资金不超过145万元,请你通过计算求出有几种购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年新冠肺炎疫情在全球蔓延,全球疫情大考面前,中国始终同各国安危与共、风雨同舟,时至5月,中国已经向150多个国家和国际组织提供医疗物质援助.某次援助,我国组织20架飞机装运口罩、消毒剂、防护服三种医疗物质共120吨,按计划20架飞机都要装运,每架飞机只能装运同一种医疗物质,且必须装满.根据下表提供的信息,解答以下问题:
防疫物质种类 | 口罩 | 消毒剂 | 防护服 |
每架飞机运载量(吨) | 8 | 5 | 4 |
每吨物资运费(元) | 1200 | 1600 | 1000 |
(1)若有9架飞机装运口罩,有![]() 架飞机装运消毒剂,求
架飞机装运消毒剂,求![]() 的值;
的值;
(2)若有![]() 架飞机装运口罩,有
架飞机装运口罩,有![]() 架飞机装运消毒剂,求
架飞机装运消毒剂,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)如果装运每种医疗物质的飞机都不少于4架,那么飞机的安排方案有几种?这些方案中,若要使此次物质运费最小,应采取哪个方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
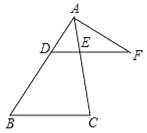
【题目】如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.
(1)如果![]() ,DE=6,求边BC的长;
,DE=6,求边BC的长;
(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=4,∠BAC=120°,AD为BC边上的高,点P从点B以每秒![]() 个单位长度的速度向终点C运动,同时点Q从点C以每秒1个单位长度的速度向终点A运动,其中一个点到达终点时,两点同时停止.
个单位长度的速度向终点C运动,同时点Q从点C以每秒1个单位长度的速度向终点A运动,其中一个点到达终点时,两点同时停止.
(1)求BC的长;
(2)设△PDQ的面积为S,点P的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围;
(3)在动点P、Q的运动过程中,是否存在PD=PQ,若存在,求出△PDQ的周长,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建设银行的某储蓄员小张在办理业务时,约定存入为正,取出为负.![]() 年
年![]() 月
月![]() 日他办理了
日他办理了![]() 件业务:
件业务:![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元.
元.
![]() 若他早上领取备用金
若他早上领取备用金![]() 元,那么下班时应交回银行多少元?
元,那么下班时应交回银行多少元?
![]() 若每办一件业务,银行发给业务量的
若每办一件业务,银行发给业务量的![]() 作为奖励,那么这天小张应得奖金多少元?
作为奖励,那么这天小张应得奖金多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=∠BCD=90°,点E为BC的中点,AE⊥DE.
(1)求证:△ABE∽△ECD;
(2)求证:AE2=AB·AD;
(3)若AB=1,CD=4,求线段AD,DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com