
【题目】如图,在平面直角坐标系xOy中,直线y=2x+n与x轴、y轴分别交于点A、B,与双曲线![]() 在第一象限内交于点C(1,m),直线CQ的解析式为:y=kx+b(k≠0)
在第一象限内交于点C(1,m),直线CQ的解析式为:y=kx+b(k≠0)

(1)求m和n的值;
(2)过x轴上的点D(3,0)作平行于y轴的直线l,分别与直线AB和双曲线![]() 交于点P、Q,求△APQ的面积.
交于点P、Q,求△APQ的面积.
(3)直接写出![]() 的解集
的解集
(4)直接写出直方程![]() 的解。
的解。
【答案】(1)m=4,n=2;(2)![]() ;(3)
;(3)![]() ;(4)x=1或x=3
;(4)x=1或x=3
【解析】
(1)把C点坐标带入反比例函数中,解出m=4,再把C点坐标代入一次函数中,解出n=2.
(2)解出一次函数和反比例函数解析式后,把x=3代入求出P点和Q点坐标,△APQ是以PQ为底,AD长为高,即可算出面积.
(3)根据数形结合![]() <0,在Q点的右边和C点的左边时,y=kx+b在
<0,在Q点的右边和C点的左边时,y=kx+b在![]() 的下方,即x<1或者x>3.
的下方,即x<1或者x>3.
(4)由数形结合在C点和Q点时候y=kx+b和![]() 相交,
相交, ![]() =0的解为x=1或x=3.
=0的解为x=1或x=3.
解:(1)把C点坐标代入反比例函数中得
![]()
解得m=4
在把C(1,4)代入一次函数中得
![]()
解得n=2
(2)由(1)知一次函数和反比例函数的解析式为
![]() 和
和![]()
则A点坐标为(-1,0)
AD=4
把x=3分别代入得
y=8和y=![]()
则P点坐标为(3,5),Q点坐标为(3,![]() )
)
则PQ=![]()
△APQ的面积=![]() =
=![]() =
=![]()
(3)![]() <0可以看成
<0可以看成
函数y=kx+b的图像在![]() 图像的下方时x的取值范围
图像的下方时x的取值范围
由图像得Q点的右边和C点的左边时,
y=kx+b的图像在![]() 的下方,
的下方,
即x<1或者x>3.
(4
y=kx+b和![]() 相交,
相交,
所以![]() =0的解为x=1或x=3.
=0的解为x=1或x=3.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=1,DE=3,∠EFB′=60°,则矩形ABCD的面积是( )
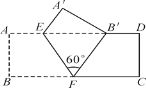
A.4B.8C.3![]() D.4
D.4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,观察由棱长为 ![]() 的小立方体摆成的图形,寻找规律:如图 ① 中,共有
的小立方体摆成的图形,寻找规律:如图 ① 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;如图 ② 中,共有
个看不见;如图 ② 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;如图 ③ 中,共有
个看不见;如图 ③ 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;
个看不见; ![]() ,则第 ⑥个图中,看得见的小立方体有________________个.
,则第 ⑥个图中,看得见的小立方体有________________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习了“求简单随机事件发生的可能性大小”知识后,小敏,小聪,小丽三人分别编写了一道有关随机事件的试题并进行了解答.小敏,小聪,小丽编写的试题分别是下面的(1)(2)(3).
(1)一个不透明的盒子里装有4个红球,2个白球,除颜色外其它都相同,搅均后,从中随意摸出一个球,摸出红球的可能性是多少?解:P(摸出一个红球)=![]() .
.
(2)口袋里装有如图所示的1角硬币2枚、5角硬币2枚、1 元硬币1枚.搅均后,从中随意摸出一枚硬币,摸出1角硬币的可能性是多少?解:P(摸出1角的硬币)=![]() .
.
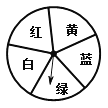
(3)如图,是一个转盘,盘面上有5个全等的扇形区域,每个区域显示有不同的颜色,轻轻转动转盘,当转盘停止后,指针对准红色区域的可能性是多少?解:P(指针对准红色区域)=![]() .
.
问题:根据以上材料回答问题:小敏,小聪,小丽三人中,谁编写的试题及解答是正确的,并简要说明其他两人所编试题或解答的不足之处.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车租赁公司准备购买A,B两种型号的新能源汽车10辆.汽车厂商提供了如下两种购买方案:
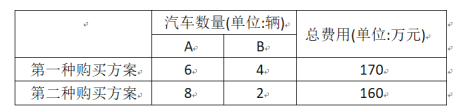
(1)A,B两种型号的新能源汽车每辆的价格各是多少万元?
(2)为了支持新能源汽车产业的发展,国家对新能源汽车发放一定的补贴.已知国家对A, B两种型号的新能源汽车补贴资金分别为每辆3万元和4万元.通过测算,该汽车租赁公司在此次购车过程中,可以获得国家补贴资金不少于34万元,公司需要支付资金不超过145万元,请你通过计算求出有几种购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
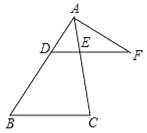
【题目】如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.
(1)如果![]() ,DE=6,求边BC的长;
,DE=6,求边BC的长;
(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要建一个面积为140平方米的仓库,仓库的一边靠墙,这堵墙长16米;在与墙平行的一边,要开一扇2米宽的门.已知围建仓库的现有木板材料可使新建板墙的总长为32米,那么这个仓库设计的长和宽应分别为多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com