
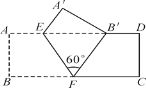
【题目】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=1,DE=3,∠EFB′=60°,则矩形ABCD的面积是( )
A.4B.8C.3![]() D.4
D.4![]()
【答案】D
【解析】
由折叠可得AE=A'E=1,∠EFB=∠EFB'=60°,根据平行线性质可得∠A'EF=120°,∠B'EF=60°,解直角三角形A'E'B'可得A'B'的长度,则可求矩形ABCD面积.
∵把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,
∴∠BFE=∠EFB'=60°,AB=A'B'∠A=∠A'=90°,AE=A'E=2,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEF=∠EFB=60°,
∵A'E∥B'F,
∴∠A'EF+∠EFB'=180°,
∴∠A'EF=120°,
∴∠A'EB'=60°且∠A'=90°,
∴∠A'B'E=30°,且A'E=1,
∴B'E=2,A'B'=![]() =AB,
=AB,
∵AE=1,DE=3,
∴AD=4,
∴S矩形ABCD=AB×AD=4×![]() =4
=4![]() ,
,
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,已知□AOBC的顶点O(0,0),![]() ,点B(12,0),按以下步骤作图:①以点O为圆心、适当长度为半径作弧,分别交OA、OB于点D,E;②分别以点D,E为圆心、大于
,点B(12,0),按以下步骤作图:①以点O为圆心、适当长度为半径作弧,分别交OA、OB于点D,E;②分别以点D,E为圆心、大于![]() 的长为半径作弧,两弧∠AOB在内交于点F;③作射线OF,交边AC于点G,则CG的长为( )
的长为半径作弧,两弧∠AOB在内交于点F;③作射线OF,交边AC于点G,则CG的长为( )

A.6B.7C.8D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格中(每个小正方形的边长是1,小正方形的顶点叫作格点),△ABC的顶点均在格点上,请在所给平面直角坐标系中按要求画图和解答下列问题:
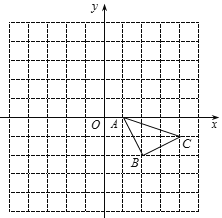
(1)以点C为旋转中心,将△ABC绕点C顺时针旋转90°得△CA1B1,画出△CA1B1;
(2)作出△ABC关于点A成中心对称的△AB2C2;
(3)设AC2与y轴交于点D,则△B1DC的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
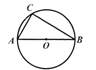
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,AB=8.
(1)利用尺规,作∠CAB的平分线,交⊙O于点D;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接CD,OD,若AC=CD,求∠B的度数;
(3)在(2)的条件下,OD交BC于点E.求出由线段ED,BE,![]() 所围成区域的面积.(其中
所围成区域的面积.(其中![]() 表示劣弧,结果保留π和根号)
表示劣弧,结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪计划中考后参加“我的中国梦”夏令营活动,需要一名家长陪同,爸爸、妈妈用猜拳的方式确定由谁陪同,即爸爸、妈妈随机做出“石头”、 “剪刀”“布” 三种手势中的一种,规定:“石头”胜“剪刀”,“剪刀” 胜“布”,“布” 胜“石头”,手势相同,不分胜负.
(1)爸爸一次出“石头”的概率是多少?
(2)妈妈一次获胜的概率是多少?请用列表或画树状图的方法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有两部不同型号的手机(分别记为A,B)和与之匹配的2个保护盖(分别记为a,b)散乱地放在桌子上.
(1)若从手机中随机取一部,再从保护盖中随机取一个,求恰好匹配的概率;
(2)若从手机和保护盖中随机取两个,用画树状图法或列表法求恰好匹配的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=2x+n与x轴、y轴分别交于点A、B,与双曲线![]() 在第一象限内交于点C(1,m),直线CQ的解析式为:y=kx+b(k≠0)
在第一象限内交于点C(1,m),直线CQ的解析式为:y=kx+b(k≠0)

(1)求m和n的值;
(2)过x轴上的点D(3,0)作平行于y轴的直线l,分别与直线AB和双曲线![]() 交于点P、Q,求△APQ的面积.
交于点P、Q,求△APQ的面积.
(3)直接写出![]() 的解集
的解集
(4)直接写出直方程![]() 的解。
的解。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批单价为4元的日用品.若按每件5元的价格销售,每月能卖出300件;若按每件6元的价格销售,每月能卖出200件,假定每月销售件数![]() (件)与价格
(件)与价格![]() (元/件)之间满足一次函数关系.
(元/件)之间满足一次函数关系.
(1)、试求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)、当销售价格定为多少时,才能使每月的利润最大?每月的最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com