
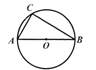
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,AB=8.
(1)利用尺规,作∠CAB的平分线,交⊙O于点D;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接CD,OD,若AC=CD,求∠B的度数;
(3)在(2)的条件下,OD交BC于点E.求出由线段ED,BE,![]() 所围成区域的面积.(其中
所围成区域的面积.(其中![]() 表示劣弧,结果保留π和根号)
表示劣弧,结果保留π和根号)
【答案】(1)作图见解析;(2)30°;(3)![]() .
.
【解析】
试题分析:(1)作AP平分∠CAB交⊙O于D;
(2)由等腰三角形性质得到∠CAD=∠ADC.又由∠ADC=∠B,得到∠CAD=∠B.
再根据角平分线定义得到∠CAD=∠DAB=∠B.由于直径所对圆周角为90°,得到∠ACB=90°,从而得到∠B的度数;
(3)先得到△OEB是30°角的直角三角形,从而得出OE,EB的长,然后把不规则图形面积转化为扇形BOD的面积减去Rt△OEB的面积求解.
试题解析:(1)如图,AP即为所求的∠CAB的平分线;
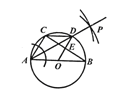
(2)∵AC=CD,∴∠CAD=∠ADC.又∵∠ADC=∠B,∴∠CAD=∠B.
∵AD平分∠CAB,∴∠CAD=∠DAB=∠B.
∵AB是⊙O的直径,∴∠ACB=90°,∴∠CAB+∠B=90°,∴3∠B=90° ,∴∠B=30°;
(3)由(2)知,∠DAB=30°.又∵∠DOB=2∠DAB,∴∠EOB=60°,∴∠OEB=90°.
在Rt△OEB中,∵OB=4,∠OBE=30°,∴OE=2,BE=![]() ,∴S=
,∴S=![]() =
=![]() =
=![]() .
.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】当今,青少年用电脑手机过多,视力水平下降已引起了全社会的关注,某校为了解八年级1000名学生的视力情况,从中抽查了150名学生的视力情况,通过数据处理,得到如下的频数分布表.解答下列问题:
视力范围分组 | 组中值 | 频数 |
3.95≤x<4.25 | 4.1 | 20 |
4.25≤x<4.55 | 4.4 | 10 |
4.55≤x<4.85 | 4.7 | 30 |
4.85≤x<5.15 | 5.0 | 60 |
5.15≤x<5.45 | 5.3 | 30 |
合计 | 150 |
(1)分别指出参加抽测学生的视力的众数、中位数所在的范围;
(2)若视力为4.85以上(含4.85)为正常,试估计该校八年级学生视力正常的人数约为多少?
(3)根据频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数相应组中的权.请你估计该校八年级学生的平均视力是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B,C三点在同一条数轴上.
(1)、若点A,B表示的数分别为-4,2,且BC=![]() AB,则点C表示的数是 ;
AB,则点C表示的数是 ;
(2)、点A,B表示的数分别为m,n,且m<n.
①若AC-AB=2,求点C表示的数(用含m,n的式子表示);
②点D是这条数轴上的一个动点,且点D在点A的右侧(不与点B重合),当AD=2AC,BC=![]() BD,求线段AD的长(用含m,n的式子表示).
BD,求线段AD的长(用含m,n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
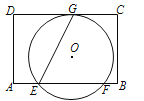
【题目】如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE=![]() AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=
AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=![]() .当边AD或BC所在的直线与⊙O相切时,AB的长是 .
.当边AD或BC所在的直线与⊙O相切时,AB的长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
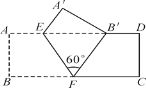
【题目】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=1,DE=3,∠EFB′=60°,则矩形ABCD的面积是( )
A.4B.8C.3![]() D.4
D.4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形.
(2)当∠ACB=30°,菱形OCED的面积为![]() ,求AC的长.
,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习了“求简单随机事件发生的可能性大小”知识后,小敏,小聪,小丽三人分别编写了一道有关随机事件的试题并进行了解答.小敏,小聪,小丽编写的试题分别是下面的(1)(2)(3).
(1)一个不透明的盒子里装有4个红球,2个白球,除颜色外其它都相同,搅均后,从中随意摸出一个球,摸出红球的可能性是多少?解:P(摸出一个红球)=![]() .
.
(2)口袋里装有如图所示的1角硬币2枚、5角硬币2枚、1 元硬币1枚.搅均后,从中随意摸出一枚硬币,摸出1角硬币的可能性是多少?解:P(摸出1角的硬币)=![]() .
.
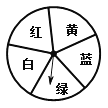
(3)如图,是一个转盘,盘面上有5个全等的扇形区域,每个区域显示有不同的颜色,轻轻转动转盘,当转盘停止后,指针对准红色区域的可能性是多少?解:P(指针对准红色区域)=![]() .
.
问题:根据以上材料回答问题:小敏,小聪,小丽三人中,谁编写的试题及解答是正确的,并简要说明其他两人所编试题或解答的不足之处.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=4,∠BAC=120°,AD为BC边上的高,点P从点B以每秒![]() 个单位长度的速度向终点C运动,同时点Q从点C以每秒1个单位长度的速度向终点A运动,其中一个点到达终点时,两点同时停止.
个单位长度的速度向终点C运动,同时点Q从点C以每秒1个单位长度的速度向终点A运动,其中一个点到达终点时,两点同时停止.
(1)求BC的长;
(2)设△PDQ的面积为S,点P的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围;
(3)在动点P、Q的运动过程中,是否存在PD=PQ,若存在,求出△PDQ的周长,若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com