
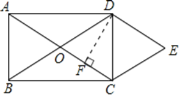
【题目】如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形.
(2)当∠ACB=30°,菱形OCED的面积为![]() ,求AC的长.
,求AC的长.

【答案】(1)证明见解析;(2)AC=4.
【解析】
(1)首先由CE∥BD,DE∥AC,可证得四边形CODE是平行四边形,又由四边形ABCD是矩形,根据矩形的性质,易得OC=OD,即可判定四边形OCED是菱形.
(2)因为∠ACB=30°可证明菱形的一条对角线和边长相等,可证明和对角线构成等边三角形,然后作辅助线,根据菱形的面积已知可求解.
(1)解:∵CE∥BD,DE∥AC,
∴四边形CODE是平行四边形,
∵四边形ABCD是矩形,
∴AC=BD,OA=OC,OB=OD,
∴OD=OC,
∴四边形OCED是菱形;
(2)解:∵∠ACB=30°,
∴∠DCO=90°-30°=60°.
又∵OD=OC,
∴△OCD是等边三角形.
过D作DF⊥OC于F,则CF=![]() OC,设CF=x,则OC=2x,AC=4x.
OC,设CF=x,则OC=2x,AC=4x.
在Rt△DFC中,tan60°=![]() ,
,
∴DF=![]() x.
x.
∴OCDF=2![]() .
.
∴x=1.
∴AC=1×4=4.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格;
![]()
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
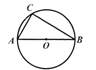
【题目】如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )

A. DE=EB B. ![]() DE=EB C.
DE=EB C. ![]() DE=DO D. DE=OB
DE=DO D. DE=OB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,AB=8.
(1)利用尺规,作∠CAB的平分线,交⊙O于点D;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接CD,OD,若AC=CD,求∠B的度数;
(3)在(2)的条件下,OD交BC于点E.求出由线段ED,BE,![]() 所围成区域的面积.(其中
所围成区域的面积.(其中![]() 表示劣弧,结果保留π和根号)
表示劣弧,结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师将1个黑球和若干个白球(这些球除颜色外都相同)放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出1个球(有放回),下表是活动进行中的一组统计数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸出黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.207 | 0.30 | 0.26 | 0.254 | 0.251 |
(1)根据上表数据估计从袋中摸出1个球是黑球的概率是_________;
(2)估计袋中白球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有两部不同型号的手机(分别记为A,B)和与之匹配的2个保护盖(分别记为a,b)散乱地放在桌子上.
(1)若从手机中随机取一部,再从保护盖中随机取一个,求恰好匹配的概率;
(2)若从手机和保护盖中随机取两个,用画树状图法或列表法求恰好匹配的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动朱老师先跑,当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是 ,因变量是 ;
(2)朱老师的速度为 米/秒;小明的速度为 米/秒;
(3)小明与朱老师相遇 次,相遇时距起点的距离分别为 米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中:
①长为![]() 的线段
的线段![]() 沿某一方向平移
沿某一方向平移![]() 后,平移后线段
后,平移后线段![]() 的长为
的长为![]() ;
;
②三角形的高在三角形内部;
③六边形的内角和是外角和的两倍;
④平行于同一直线的两直线平行;
⑤两个角的两边分别平行,则这两个角相等,真命题个数有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=(m-2)x2+(m+3)x+m+2的图象过点(0,5)
(1)求m的值,并写出二次函数的表达式;
(2)求出二次函数图象的顶点坐标、对称轴。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com