
【题目】先计算,再找出规律,然后根据规律填空.
(1)计算:
①(a-1)(a+1)=________;
②(a-1)(a2+a+1)=________;
③(a-1)(a3+a2+a+1)=________.
(2)根据(1)中的计算,用字母表示出你发现的规律.
(3)根据(2)中的结论,直接写出结果:
①(a-1)(a9+a8+a7+a6+a5+a4+a3+a2+a+1)=_____________________
②若(a-1)·M=a15-1,则M=_____________________
③(a-b)(a5+a4b+a3b2+a2b3+ab4+b5)=_____________________
④(2x-1)(16x4+8x3+4x2+2x+1)=_____________________
【答案】(1)①![]() ,②
,②![]() ,③
,③![]() ;(2)规律为:(a-1)(
;(2)规律为:(a-1)(![]() +
+![]() +... +a+1)=
+... +a+1)=![]() ;(3)①
;(3)①![]() ,② (a-1)(
,② (a-1)(![]() +
+![]() +
+![]() +
+![]() ... +
... +![]() a+1),③
a+1),③![]() ,④32x51.
,④32x51.
【解析】
(1)利用平方差公式化简即可得出①的结果;根据多项式乘以多项式运算法则加以计算即可得出②、③的结果;
(2)根据(1)中的结果,进一步归纳总结得出规律即可;
(3)根据(2)中得出的规律进一步计算即可.
(1)①(a-1)(a+1)=![]() ;
;
②(a-1)(a2+a+1)=![]() ;
;
③(a-1)(a3+a2+a+1)=![]() ;
;
故答案为:①![]() ,②
,②![]() ,③
,③![]() ;
;
(2)∵ (a-1)(a+1)=![]() ,
,
(a-1)(a2+a+1)=![]() ,
,
(a-1)(a3+a2+a+1)![]() ,
,
∴规律为:(a-1)(![]() +
+![]() +... +a+1)=
+... +a+1)=![]() ,
,
(3)由(2)可知:(a-1)(![]() +
+![]() +... +a+1)=
+... +a+1)=![]() ,
,
①∴(a-1)(a9+a8+a7+a6+a5+a4+a3+a2+a+1)=![]() ,
,
故答案为:![]() ;
;
②∵(a-1)·M=a15-1,
∴M=(a-1)(![]() +
+![]() +
+![]() +
+![]() ... +
... +![]() a+1),
a+1),
故答案为:(a-1)(![]() +
+![]() +
+![]() +
+![]() ... +
... +![]() a+1);
a+1);
③(a-b)(a5+a4b+a3b2+a2b3+ab4+b5)=![]() ,
,
故答案为:![]() ;
;
④(2x1)(16x4+8x3+4x2+2x+1)=(2x1)[( 2x) 4+ (2x)3+ (2x)2+2x+1]= ( 2x) 5-1=32x51,
故答案为:32x51.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
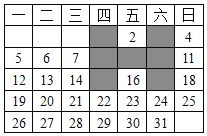
【题目】如图,表中给出的是某月的月历,任意选取“![]() ”型框中的
”型框中的![]() 个数(如阴影部分所示).请你运用所学的数学知识来研究,则这
个数(如阴影部分所示).请你运用所学的数学知识来研究,则这![]() 个数的和不可能是( )
个数的和不可能是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有2个红球1个黄球,这3个小球除颜色不同外,其它都相同,贝贝同学摸出一个球后放回口袋再摸一个;莹莹同学一次摸2个球,两人分别记录下小球的颜色,关于两人摸到1个红球1个黄球和2个红球的概率的描述中,正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小梅将边长分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …长的若干个正方形按一定规律拼成不同的长方形,如图所示.
…长的若干个正方形按一定规律拼成不同的长方形,如图所示.
![]() 求第四个长方形的周长;
求第四个长方形的周长;
![]() 当
当![]() 时,求第五个长方形的面积.(用科学记数法表示)
时,求第五个长方形的面积.(用科学记数法表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知 AD 是△ABC 的边 BC 上的中线.
(1)作出△ABD 的边 BD 上的高.
(2)若△ABC 的面积为 10,求△ADC 的面积.
(3)若△ABD 的面积为 6,且 BD 边上的高为 3,求 BC 的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
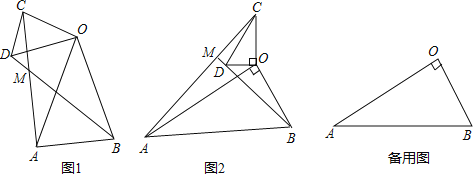
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的个数有( )
①绝对值最小的有理数是0;②两个有理数比较大小,绝对值大的反而小;③用一个平面去截一个正方体,截面可能是六边形;④有理数分为正有理数和负有理数;⑤在数轴上,与表示3的点的距离等于4的点所表示的数为7;⑥当![]() 时,
时,![]() .
.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠AOB.
求作:∠A'O'B',使∠A'O′B'=∠AOB
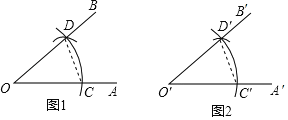
(1)如图1,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C、D;
(2)如图2,画一条射线O′A′,以点O′为圆心,OC长为半径间弧,交O′A′于点C′;
(3)以点C′为圆心,CD长为半径画弧,与第2步中所而的弧交于点D′;
(4)过点D′画射线O′B',则∠A'O'B'=∠AOB.
根据以上作图步骤,请你证明∠A'O'B′=∠AOB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣![]() x2+bx+c的图象经过A(0,3),B(﹣4,﹣
x2+bx+c的图象经过A(0,3),B(﹣4,﹣![]() )两点.
)两点.
(1)求b,c的值.
(2)二次函数y=﹣![]() x2+bx+c的图象与x轴是否有公共点,求公共点的坐标;若没有,请说明情况.
x2+bx+c的图象与x轴是否有公共点,求公共点的坐标;若没有,请说明情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com