
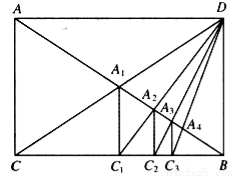
对于任意线AB,可以构造以AB为对角线的矩形ACBD,连接CD,与AB交于A1点,过A1作BC的垂线段A1C1,垂足为C1;连接C1D,与AB交于A2点,过A2作BC的垂线段A2C2,垂足为C2;连接C2D,与AB交于A3点,过A3点作BC的垂线段A3C3,垂足为C3……。如此下去,可以依次得到点A4,A5,…,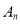 ,如果设AB的长为1,依次可求得A1B,A2B,A3B,……的长,则
,如果设AB的长为1,依次可求得A1B,A2B,A3B,……的长,则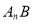 的长用
的长用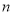 的代数式表示为
的代数式表示为
A.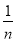 B.
B.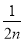 C.
C.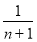 D.
D.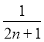
科目:初中数学 来源:2015年广东省汕头市金平区中考模拟数学试卷(解析版) 题型:选择题
如图,在等腰三角形纸片ABC中,AB=AC,∠A=40°,折叠该纸片,使点A落在点B处,折痕为DE,则∠CBE的度数是()
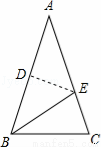
A.20° B.30° C.40° D.70°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省阶段教育学校招生适应性考试数学试卷(解析版) 题型:解答题
(本小题满分7分)
(本题共2个小题,第1小题3分,第2小题4分,共7分)
(1)4sin60°-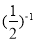 -2
-2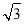 -
-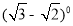
(2)先化简,再求值:(2a+b)(2a-b)+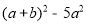 ,其中a=6,b=-
,其中a=6,b=-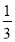 .
.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级学业水平模拟数学试卷(解析版) 题型:解答题
已知直线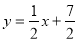 与茹
与茹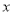 、
、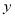 轴分别相交于B,A两点,抛物线
轴分别相交于B,A两点,抛物线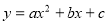 过A,B两点,且对称轴为直线
过A,B两点,且对称轴为直线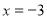 .
.
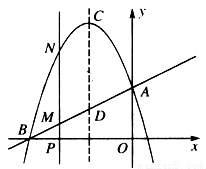
(1)求A,B两点的坐标,并求抛物线的解析式;
(2)若点P以1个单位/秒的速度从点B沿 轴向点O运动.过点P作
轴向点O运动.过点P作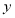 轴的平行线交直线AB于点M,交抛物线于点N.设点P运动的时间为
轴的平行线交直线AB于点M,交抛物线于点N.设点P运动的时间为 ,MN的长度为S,求S与
,MN的长度为S,求S与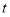 之间的函数关系式,并求出当
之间的函数关系式,并求出当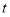 为何值时,S取得最大值?
为何值时,S取得最大值?
(3)设抛物线的对称轴CD与直线AB相交于点D,顶点为C.问:在(2)条件不变情况下,是否存在一个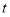 值,使四边形CDMN是平行四边形?若存在,求出
值,使四边形CDMN是平行四边形?若存在,求出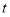 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级学业水平模拟数学试卷(解析版) 题型:填空题
如图,半径为2 cm,圆心角为90°的扇形OAB的弧上有一运动的点P.从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为___________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级学业水平模拟数学试卷(解析版) 题型:选择题
某校九年级四个班的代表队准备举行篮球友谊赛.甲、乙、丙三位同学预测比赛的 结果如下:
甲说:“902班得冠军,904班得第三”;
乙说:“901班得第四,903班得亚军”;
丙说:“903班得第三,904班得冠军”.
赛后得知,三人都只猜对了一半,则得冠军的是
A.901班 B.902班 C.903班 D.904班
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级中考适应性测试四数学试卷(解析版) 题型:解答题
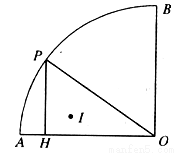
如图,在正方形ABCD中, AB=5,P是BC边上任意一点,E是BC延长线上一点,连接AP,作PF⊥AP,使PF=PA,连接CF,AF,AF交CD边于点G,连接PG.
(1)求证:∠GCF=∠FCE;
(2)判断线段PG,PB与DG之间的数量关系,并证明你的结论;
(3)若BP=2,在直线AB上是否存在一点M,使四边形DMPF是平行四边形,若存在,求出BM的长度,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级中考适应性测试四数学试卷(解析版) 题型:选择题
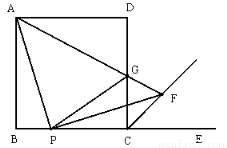
如图,在等边△ABC中,点D、E分别是边AB、AC的中点.将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是
A.矩形 B.菱形 C.正方形 D.梯形
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省武城县九年级学业水平第一次模拟考试数学试卷(解析版) 题型:填空题
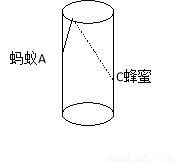
如图圆柱形玻璃杯高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁A,离杯口上沿4cm与蜜蜂相对的点A处,则蚂蚁到达蜂蜜的最短距离为_______________cm。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com