
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.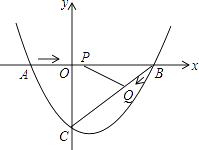
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.
【答案】
(1)解:把点A(﹣2,0)、B(4,0)分别代入y=ax2+bx﹣3(a≠0),得
![]() ,
,
解得 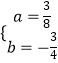 ,
,
所以该抛物线的解析式为:y= ![]() x2﹣
x2﹣ ![]() x﹣3;
x﹣3;
(2)解:设运动时间为t秒,则AP=3t,BQ=t.
∴PB=6﹣3t.
由题意得,点C的坐标为(0,﹣3).
在Rt△BOC中,BC= ![]() =5.
=5.
如图1,过点Q作QH⊥AB于点H.
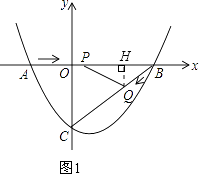
∴QH∥CO,
∴△BHQ∽△BOC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴HQ= ![]() t.
t.
∴S△PBQ= ![]() PBHQ=
PBHQ= ![]() (6﹣3t)
(6﹣3t) ![]() t=﹣
t=﹣ ![]() t2+
t2+ ![]() t=﹣
t=﹣ ![]() (t﹣1)2+
(t﹣1)2+ ![]() .
.
当△PBQ存在时,0<t<2
∴当t=1时,
S△PBQ最大= ![]() .
.
答:运动1秒使△PBQ的面积最大,最大面积是 ![]() ;
;
(3)解:设直线BC的解析式为y=kx+c(k≠0).
把B(4,0),C(0,﹣3)代入,得
![]() ,
,
解得 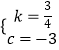 ,
,
∴直线BC的解析式为y= ![]() x﹣3.
x﹣3.
∵点K在抛物线上.
∴设点K的坐标为(m, ![]() m2﹣
m2﹣ ![]() m﹣3).
m﹣3).
如图2,过点K作KE∥y轴,交BC于点E.则点E的坐标为(m, ![]() m﹣3).
m﹣3).
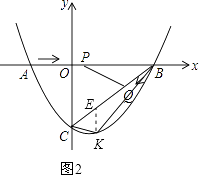
∴EK= ![]() m﹣3﹣(
m﹣3﹣( ![]() m2﹣
m2﹣ ![]() m﹣3)=﹣
m﹣3)=﹣ ![]() m2+
m2+ ![]() m.
m.
当△PBQ的面积最大时,∵S△CBK:S△PBQ=5:2,S△PBQ= ![]() .
.
∴S△CBK= ![]() .
.
S△CBK=S△CEK+S△BEK= ![]() EKm+
EKm+ ![]() EK(4﹣m)
EK(4﹣m)
= ![]() ×4EK
×4EK
=2(﹣ ![]() m2+
m2+ ![]() m)
m)
=﹣ ![]() m2+3m.
m2+3m.
即:﹣ ![]() m2+3m=
m2+3m= ![]() .
.
解得 m1=1,m2=3.
∴K1(1,﹣ ![]() ),K2(3,﹣
),K2(3,﹣ ![]() ).
).
【解析】方法二:(1)略.(2)设运动时间为t秒,则AP=3t,BQ=t,PB=6﹣3t,
∴点C的坐标为(0,﹣3),
∵B(4,0),∴lBC:y= ![]() x﹣3,
x﹣3,
过点Q作QH⊥AB于点H,
∴tan∠HBQ= ![]() ,∴sin∠HBQ=
,∴sin∠HBQ= ![]() ,
,
∵BQ=t,∴HQ= ![]() t,
t,
∴S△PBQ= ![]() PBHQ=
PBHQ= ![]() =﹣
=﹣ ![]() ,
,
∴当t=1时,S△PBQ最大= ![]() .
.
⑶过点K作KE⊥x轴交BC于点E,
∵S△CBK:S△PBQ=5:2,S△PBQ= ![]() ,
,
∴S△CBK= ![]() ,
,
设E(m, ![]() m﹣3),K(m,
m﹣3),K(m, ![]() ),
),
S△CBK= ![]() =
= ![]() =﹣
=﹣ ![]() ,
,
∴﹣ ![]() =
= ![]() ,
,
∴m1=1,m2=3,
∴K1(1,﹣ ![]() ),K2(3,﹣
),K2(3,﹣ ![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,且EG、FH交于点O.若AC=4,则EG2+FH2=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PC=2PB.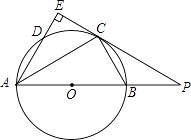
(1)探究线段PB,AB之间的数量关系,并说明理由;
(2)若AD=3,求AB长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=![]() x与直线l2交点A的横坐标为2,将直线l1沿y轴向下平移4个单位长度,得到直线l3,直线l3与y轴交于点B,与直线l2交于点C,点C的纵坐标为-2.直线l2与y轴交于点D.
x与直线l2交点A的横坐标为2,将直线l1沿y轴向下平移4个单位长度,得到直线l3,直线l3与y轴交于点B,与直线l2交于点C,点C的纵坐标为-2.直线l2与y轴交于点D.
(1)求直线l2的解析式;
(2)求△BDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点.
(1)若∠BAC=60°,∠C=70°,求∠AFB的大小;
(2)若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副扑克牌中的三张黑桃牌(它们的正面数字分别为3、4、5)洗匀后正面朝下放在桌面上.小王和小李玩摸牌游戏,游戏规则如下:先由小王随机抽取一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小李随机抽取一张牌,记下牌面数字.当两张牌的牌面数字相同时,小王赢;当两张牌的牌面数字不同时,小李赢.现请你分析游戏规则对双方是否公平,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知, 四边形![]() , 连接
, 连接![]() ,
,![]() ,
,![]() .
.
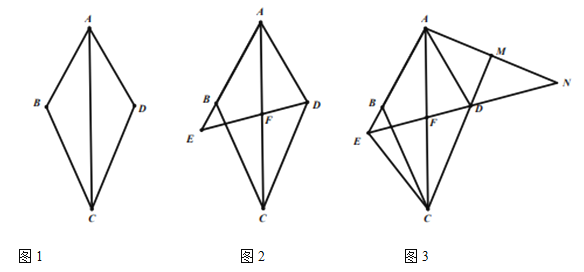
(1)如图![]() , 求证:
, 求证:![]() 平分
平分![]() ;
;
(2)如图![]() ,点
,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在![]() 的条件下,连接
的条件下,连接![]() ,点
,点![]() 在
在![]() 延长线上,连接
延长线上,连接![]() ,延长
,延长![]() 与
与![]() 延长线交于点
延长线交于点![]() , 若
, 若![]() ,
,![]() ,
, ![]() 的面积与
的面积与![]() 的面积比为
的面积比为![]() ,
, ![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)如图1,锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE交于F,连DE,求证:DFDA=DBDC;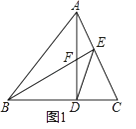
(2)如图2,若∠BAC=90°,AD⊥BC于D,F为线段AD上一点,在AD延长线上找一点G使AD2=DFDG,请画出图形找出点G并加以证明;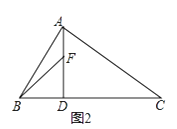
(3)如图3,在(1)的条件下,若∠ABC=45°,EF=1,EC=3,直接写出BD长.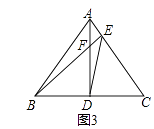
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com