
【题目】综合题
(1)如图1,锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE交于F,连DE,求证:DFDA=DBDC;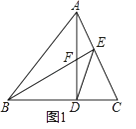
(2)如图2,若∠BAC=90°,AD⊥BC于D,F为线段AD上一点,在AD延长线上找一点G使AD2=DFDG,请画出图形找出点G并加以证明;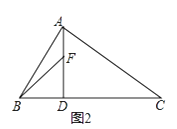
(3)如图3,在(1)的条件下,若∠ABC=45°,EF=1,EC=3,直接写出BD长.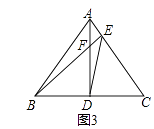
【答案】
(1)解:证明:如图1中,
∵AD、AE是△ABC的高,
∴∠ADC=∠BDF=∠BEC=90°,
∴∠DBF+∠C=90°,∠DAC+∠C=90°,
∴∠DBF=∠DAC,
∴△DBF∽△DAC,
∴ ![]() =
= ![]() ,
,
∴DFDA=DBDC.
(2)解:如图2中,在DC上截取DM,使得DM=DA,
连接FM、AM,作MN⊥FM交AD的延长线于G.则AD2=DFDG.
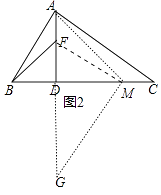
理由:∵∠MDF=∠MDG=∠FMG=90°,
∴∠DMF+∠DMG=90°,∠DMG+∠G=90°,
∴∠DMF=∠G,
∴△DMF∽△DGM,
∴ ![]() =
= ![]() ,
,
∴DM2=DFDG,
∵AD=DM,
∴AD2=DFDG.
(3)解:如图3中,连接FC.
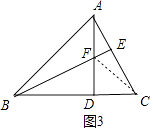
∵∠ABC=45°,∠ADB=90°,
∴BD=AD,
∵∠DBF=∠CAD(已证),∠BDF=∠ADC=90°,
∴△BDF≌△ADC,
∴DF=DC,
在Rt△EFC中,FC= ![]() =
= ![]() =
= ![]() ,
,
∴DF=DC= ![]() ,设BD=AD=y,则AC=
,设BD=AD=y,则AC= ![]() =
= ![]() ,
,
∵△EAF∽△DAC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得y=2 ![]() 或
或 ![]() (舍弃),
(舍弃),
∴BD=2 ![]() .
.
【解析】(1)先证明∠DBF=∠DAC,然后再证明△DBF∽△DAC,最后,依据相似三角形对应边成比例求解即可;
(2)在DC上截取DM,使得DM=DA,连接FM、AM,作MN⊥FM交AD的延长线于G.则AD2=DFDG.接下来,再证明△DMF∽△DGM即可解决问题;
(3)连接FC.依据ASA可证明△BDF≌△ADC,根据全等三角形的性质定理可得到DF=DC,接下来,依据勾股定理可求得DF、DC的长,设BD=AD=y,则可得到AC的长,最后,依据△EAF∽△DAC,可得到关于y的比例式,从而可求得y的值.
【考点精析】掌握相似三角形的应用是解答本题的根本,需要知道测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.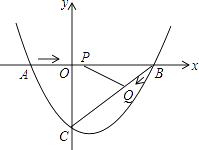
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要得到△ABD≌△ACE,从下列条件中补选一个,则错误的是( )

A.AB=AC B.DB=EC C.∠ADB=∠AEC D.∠B=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,成都市青羊区有一块长为![]() 米,宽为
米,宽为![]() 米的长方形地块,角上有四个边长均为
米的长方形地块,角上有四个边长均为![]() 米的小正方形空地,开发商计划将阴影部分进行绿化.
米的小正方形空地,开发商计划将阴影部分进行绿化.
(1)用含![]() ,
,![]() 的代数式表示绿化的面积是多少平方米?(结果写成最简形式)
的代数式表示绿化的面积是多少平方米?(结果写成最简形式)
(2)若![]() ,
,![]() ,求出绿化面积.
,求出绿化面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知1辆甲型客车和1辆乙型客车共可载客75人.已知1辆甲型客车和2辆乙型客车共可载客105人.某学校计划租用两种型号客车送234名学生和6名老师集体外出活动.从安全角度考虑每辆车上至少要有1名老师,并且总费用不超过2280元.
(1)求每辆甲型客车和每辆乙型客车分别可载多少人?
(2)共需租辆客车?
(3)若每辆甲型客车和每辆乙型客车的租金分别为400元和280元,设租甲型客车x辆,总费用为W元,请你给出最节省的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:对任意一个三位数![]() 如果
如果![]() 满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与
满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与![]() 的商记为
的商记为![]() .例如
.例如![]() 对调百位与十位上的数字得到
对调百位与十位上的数字得到![]() 对调百位与个位上的数字得到
对调百位与个位上的数字得到![]() 对调十位与个位上的数字得到
对调十位与个位上的数字得到![]() 这三个新三位数的和为
这三个新三位数的和为![]() 所以
所以![]() .试根据以上信息,完成下列问题:
.试根据以上信息,完成下列问题:
(1)计算:![]() __,
__,![]() __,你从中发现什么规律?你发现规律是:__.
__,你从中发现什么规律?你发现规律是:__.
(2)若![]() 都是“相异数”,
都是“相异数”,![]()
![]() ,其中x是正整数),是否存在
,其中x是正整数),是否存在![]() 满足
满足![]() ,若存在,请求出这个
,若存在,请求出这个![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家快餐店销售![]() 三种套餐,其中
三种套餐,其中![]() 套餐包含一荤两素,
套餐包含一荤两素,![]() 套餐包含两荤一素,
套餐包含两荤一素,![]() 套餐包含两荤两素,每份套餐中一荤的成本相同,一素的成本也相同,已知一份
套餐包含两荤两素,每份套餐中一荤的成本相同,一素的成本也相同,已知一份![]() 套餐的售价是一份
套餐的售价是一份![]() 套餐和一份
套餐和一份![]() 套餐售价之和的
套餐售价之和的![]() 一天下来,店长发现
一天下来,店长发现![]() 套餐和
套餐和![]() 套餐的销量相同,且
套餐的销量相同,且![]() 套餐的利润和是
套餐的利润和是![]() 套餐利润的两倍,当天的总利润率是
套餐利润的两倍,当天的总利润率是![]() .第二天店内搞活动,
.第二天店内搞活动,![]() 套餐的售价打五折,
套餐的售价打五折,![]() 套餐的售价均不变,当
套餐的售价均不变,当![]() 三种套餐的销量相同时,总利润率为________.
三种套餐的销量相同时,总利润率为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com