
【题目】如图,在⊙O中,AC是弦,AD是切线,CB⊥AD于B,CB与⊙O相交于点E,连接AE,若AE平分∠BAC,BE=1,则CE= . 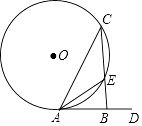
科目:初中数学 来源: 题型:
【题目】综合题
(1)如图1,锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE交于F,连DE,求证:DFDA=DBDC;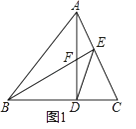
(2)如图2,若∠BAC=90°,AD⊥BC于D,F为线段AD上一点,在AD延长线上找一点G使AD2=DFDG,请画出图形找出点G并加以证明;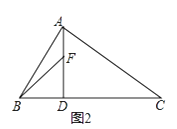
(3)如图3,在(1)的条件下,若∠ABC=45°,EF=1,EC=3,直接写出BD长.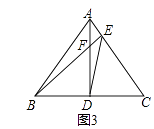
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】玲玲和牛牛相约在小区笔直的步行道上健步走锻炼身体.两人都从步行道起点![]() 向终点
向终点![]() 走去.牛牛出发
走去.牛牛出发![]() 分钟后,玲玲出发.又过了
分钟后,玲玲出发.又过了![]() 分钟,牛牛停下来接了
分钟,牛牛停下来接了![]() 分钟的电话,玲玲则以原速继续步行,与牛牛相遇后,玲玲的速度减少到原来的
分钟的电话,玲玲则以原速继续步行,与牛牛相遇后,玲玲的速度减少到原来的![]() 走向终点
走向终点![]() .牛牛接完电话后,提高速度向终点
.牛牛接完电话后,提高速度向终点![]() 走去,
走去,![]() 分钟后刚好追上玲玲,到达终点
分钟后刚好追上玲玲,到达终点![]() 后立即调头以提速后的速度返回起点
后立即调头以提速后的速度返回起点![]() (调头时间忽略不计),玲玲、牛牛两人相距的路程
(调头时间忽略不计),玲玲、牛牛两人相距的路程![]() (米)与牛牛出发的时间
(米)与牛牛出发的时间![]() (分钟)之间的关系如图所示.
(分钟)之间的关系如图所示.

(1)牛牛开始健步走的速度为_______米/分;
(2)求玲玲开始健步走的速度和牛牛提速后的速度;
(3)玲玲走到终点![]() 后,停下来休息了一会儿.牛牛回到起点
后,停下来休息了一会儿.牛牛回到起点![]() 后,立即调头仍以提速后的速度走向终点
后,立即调头仍以提速后的速度走向终点![]() ,玲玲休息
,玲玲休息![]() 分钟后以减速后的速度调头走向起点
分钟后以减速后的速度调头走向起点![]() 两人恰好在
两人恰好在![]() 中点处相遇,求步行道
中点处相遇,求步行道![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长为( )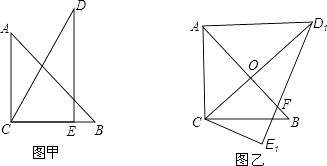
A.![]()
B.5
C.4
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD,AE,AF分别为△ABC的高线、角平分线和中线.

(1)写出图中所有相等的角和相等的线段;
(2)当BF=8cm,AD=7 cm时,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD,点E在AD边上,DE>AE,连接BE,将△ABE沿着BE翻折得到△BFE,射线EF交BC于G,若点G为BC的中点,FG=1,DE=6,则AE的长 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
关于x的方程:![]() 的解是
的解是![]() ,
,![]() ;
;![]() 即
即![]() 的解是
的解是![]() ;
;![]() 的解是
的解是![]() ,
,![]() ;
;![]() 的解是
的解是![]() ,
,![]() ;
;![]()
![]() 请观察上述方程与解的特征,比较关于x的方程
请观察上述方程与解的特征,比较关于x的方程![]() 与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.
与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.
![]() 由上述的观察、比较、猜想、验证,可以得出结论:
由上述的观察、比较、猜想、验证,可以得出结论:
如果方程的左边是未知数与其倒数的倍数的和,方程的右边的形式与左边完全相同,只是把其中的未知数换成了某个常数,那么这样的方程可以直接得解,请用这个结论解关于x的方程:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com