
分析 (1)根据y与x成正比例,可设y=kx,把x=5,y=6代入,用待定系数法可求出函数解析式;
(2)将点(3,6)与点($\frac{1}{2}$,-$\frac{1}{2}$)分别代入y=kx+b,组成关于k、b的二元一次方程组,解方程组即可求出k、b的值,从而得到直线的解析式.
解答 解:(1)设y=kx,把x=5,y=6代入,
得5k=6,解得k=$\frac{6}{5}$,
故所求函数解析式为y=$\frac{6}{5}$x;
(2)∵直线y=kx+b经过点(3,6)与点($\frac{1}{2}$,-$\frac{1}{2}$),
∴$\left\{\begin{array}{l}{3k+b=6}\\{\frac{1}{2}k+b=-\frac{1}{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{13}{5}}\\{b=-\frac{9}{5}}\end{array}\right.$,
∴所求函数解析式为y=$\frac{13}{5}$x-$\frac{9}{5}$.
点评 本题考查了待定系数法求一次函数与正比例函数的解析式,熟练掌握待定系数法是解题的关键.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x6÷x3=x2 | B. | (-1)-1=-1 | C. | 4m-2=$\frac{1}{{4{m^2}}}$ | D. | (a2)4=a6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
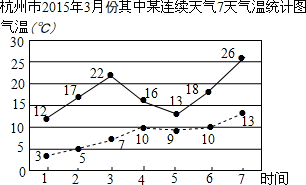 如图是2015年3月份其中某连续7天气温的统计图,其中实线表示最高气温,虚线表示最低气温,在下列结论中(某天中最高气温与最低气温的差值叫做温差):
如图是2015年3月份其中某连续7天气温的统计图,其中实线表示最高气温,虚线表示最低气温,在下列结论中(某天中最高气温与最低气温的差值叫做温差):| A. | ①②③④ | B. | ①② | C. | ①③ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com