
【题目】综合与实践:折纸中的数学
动手操作:
如图,将矩形ABCD折叠,点B落在AD边上的点B′处,折痕为GH,再将矩形ABCD折叠,点D落在B′H的延长线上,对应点为D′,折痕为B′E,延长GH于点F,O为GE的中点.
数学思考: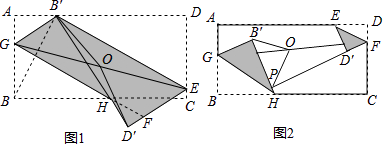
(1)猜想:线段OB′与OD′的数量关系是(不要求说理或证明).
(2)求证:四边形GFEB′为平行四边形;
(3)拓展探究:
如图2,将矩形ABCD折叠,点B对应点B′,点D对应点为D′,折痕分别为GH、EF,∠BHG=∠DEF,延长FD′交B′H于点P,O为GF的中点,试猜想B′O与OP的数量关系,并说明理由.
【答案】
(1)OB′=OD′
(2)
解:如图1,
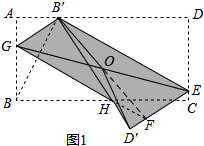
由折叠得:∠GHB=∠GHB′= ![]() ∠B′HB,
∠B′HB,
∠DB′E=∠D′B′E= ![]() ∠D′B′D,
∠D′B′D,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠B′HB=′DB′D′,
∴∠GHB′=∠EB′H,
∴GF∥B′E,
∵∠GB′H=∠B=90°,∠B′D′E=∠D=90°,
∴∠GB′H=∠B′D′E,
∴GB′∥EF,
∴四边形GB′EF为平行四边形;
(3)
解:如图2,
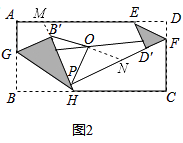
OB′=OP,理由是:
延长HB′交AD于M,延长B′O交D′P于点N,
∠B′HB=2∠GHB,∠DED′=2∠DEF,∠GHB=∠DEF,
∴∠B′HB=∠DED′,
∵AD∥BC,∠DMH=∠B′HB,
∴∠DED′=∠DMH,
∴ED′∥MH,
∴∠B′PN=∠ED′F=90°,
∴∠GB′P=∠B′PN,
∴GB′∥PD′,
∴∠B′GO=∠NFO,
∵∠GOB′=∠FON,GO=OF,
∴△GB′O≌△FNO,
∴B′O=NO,
∴B′O=OP.
【解析】解:(1)如图1,OB′=OD′,理由是:
连接OF,
由折叠得:∠GB′H=∠B=90°,∠B′D′E=∠D=90°,
∴∠GB′H=∠B′D′E,
∴GB′∥EF,
同理得B′E∥GF,
∴四边形GFEB′是平行四边形,
∴OB′=OF,
则B′、O、F共线,
在Rt△B′D′F中,OD′= ![]() B′F=OB′,
B′F=OB′,
即OB′=OD′;
【考点精析】利用平行四边形的判定与性质对题目进行判断即可得到答案,需要熟知若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如果二次函数的二次项系数为l,则此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].
(1)若一个函数的特征数为[﹣2,1],求此函数图象的顶点坐标.
(2)探究下列问题: ①若一个函数的特征数为[4,﹣1],将此函数的图象先向右平移1个单位,再向上平移1个单位,求得到的图象对应的函数的特征数.
②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的两条中线AD、CE交于点G,且AD⊥CE,联结BG并延长与AC交于点F,如果AD=9,CE=12,那么下列结论不正确的是( )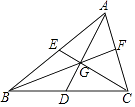
A.AC=10
B.AB=15
C.BG=10
D.BF=15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点D位于△ABC边AC上,已知AB是AD与AC的比例中项. 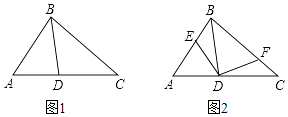
(1)求证:∠ACB=∠ABD;
(2)现有点E、F分别在边AB、BC上如图2,满足∠EDF=∠A+∠C,当AB=4,BC=5,CA=6时,求证:DE=DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6. 
(1)实践操作:尺规作图,不写作法,保留作图痕迹. ①作∠ABC的角平分线交AC于点D.
②作线段BD的垂直平分线,交AB于点E,交BC于点F,连接DE、DF.
(2)推理计算:四边形BFDE的面积为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列正方形网格的每个小正方形的边长均为1,⊙O的半径为n≥8 ![]() .规定:顶点既在圆上又是正方形格点的直角三角形称为“圆格三角形”,请按下列要求各画一个“圆格三角形”,并用阴影表示出来.
.规定:顶点既在圆上又是正方形格点的直角三角形称为“圆格三角形”,请按下列要求各画一个“圆格三角形”,并用阴影表示出来.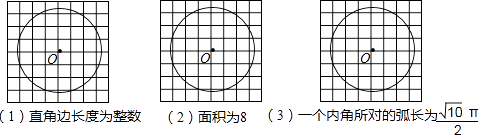
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环还需要的正五边形个数是( ) 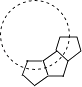
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+c的图象经过点A(m,0)、B(0,n),其中m、n是方程x2﹣6x+5=0的两个实数根,且m<n.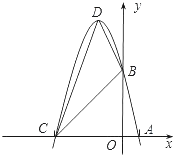
(1)求抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一个交点为C,抛物线的顶点为D,求C、D点的坐标和△BCD的面积;
(3)P是线段OC上一点,过点P作PH⊥x轴,交抛物线于点H,若直线BC把△PCH分成面积相等的两部分,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某跳水队为了解运动员的年龄情况,作了一次年龄调查,根据跳水运动员的年龄(单位:岁),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
(1)本次接受调查的跳水运动员人数为 , 图①中m的值为;
(2)求统计的这组跳水运动员年龄数据的平均数、众数和中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com