
【题目】如图,已知△ABC中,∠A=∠ACB,CD是∠ACB的平分线,∠ADC=150°,则∠ABC的度数为_____度.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:
【题目】小明和小颖在如图所示的四边形场地上,沿边骑自行车进行场地追逐赛(两人只要有一个人回到自己的出发点,则比赛结束).小明从A地出发,沿A→B→C→D→A的路线匀速骑行,速度为8米/秒;小颖从B地出发,沿B→C→D→A→B的路线匀速骑行,速度为6米/秒.已知∠ABC=90°,AB=40米,BC=80米,CD=90米.设骑行时间为t秒,假定他们同时出发且每转一个弯需要额外耗时2秒.
(1)填空:当t=_____秒时,两人第一次到B地的距离相等;
(2)试问小明能否在小颖到达D地前追上她?若能,求出此时t的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是高,CE是中线,点G是CE的中点,DG⊥CE,点G为垂足. 
(1)求证:DC=BE;
(2)若∠AEC=66°,求∠BCE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线m⊥n.在平面直角坐标系xOy中,x轴∥m,y轴∥n.如果以O1为原点,点A 的坐标为(1,1).将点O1平移2 ![]() 个单位长度到点O2 , 点A的位置不变,如果以O2为原点,那么点A的坐标可能是( )
个单位长度到点O2 , 点A的位置不变,如果以O2为原点,那么点A的坐标可能是( )
A.(3,﹣1)
B.(1,﹣3)
C.(﹣2,﹣1)
D.(2 ![]() +1,2
+1,2 ![]() +1)
+1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,PC切⊙O于点C,AB的延长线与PC交于点P,PC的延长线与AD交于点D,AC平分∠DAB. 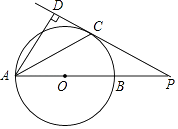
(1)求证:AD⊥PC;
(2)连接BC,如果∠ABC=60°,BC=2,求线段PC的长. 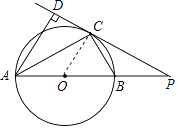
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有客房50间,当每间客房每天的定价为220元时,客房会全部住满;当每间客房每天的定价增加10元时,就会有一间客房空闲,设每间客房每天的定价增加x元时,客房入住数为y间.
(1)求y与x的函数关系式(不要求写出x的取值范围);
(2)如果每间客房入住后每天的各种支出为40元,不考虑其他因素,则该宾馆每间客房每天的定价为多少时利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com