
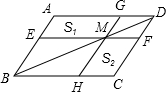
 如图,过平行四边形ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的过平行四边形AEMG的面积S1与?HCFM的面积S2的大小关系是( )
如图,过平行四边形ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的过平行四边形AEMG的面积S1与?HCFM的面积S2的大小关系是( )| A. | S1>S2 | B. | S1=S2 | C. | S1<S2 | D. | 不能确定 |
分析 根据平行四边形的性质和判定得出平行四边形GBEP、GPFD,证△ABD≌△CDB,得出△ABD和△CDB的面积相等;同理得出△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,相减即可求出答案.
解答 解:∵四边形ABCD是平行四边形,EF∥BC,HG∥AB,
∴AD=BC,AB=CD,AB∥GH∥CD,AD∥EF∥BC,
∴四边形HBEM、GMFD是平行四边形,
在△ABD和△CDB中;,
$\left\{\begin{array}{l}{AB=CD}\\{BD=DB}\\{DA=CB}\end{array}\right.$,
∴△ABD≌△CDB(SSS),
即△ABD和△CDB的面积相等;
同理△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,
故四边形AEMG和四边形HCFM的面积相等,即S1=S2.
故选:B.
点评 本题考查了平行四边形的性质和判定,全等三角形的性质和判定的应用,解此题的关键是求出△ABD和△CDB的面积相等,△BEP和△PGB的面积相等,△HPD和△FDP的面积相等,注意:如果两三角形全等,那么这两个三角形的面积相等.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
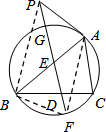 如图,△ABC内接于⊙O,过BC的中点D作直线l∥AC,l与AB交于点E,与⊙O交于点G、F,与⊙O在点A处的切线交于点P,若PE=3,ED=2,EF=3,则PA的长度为( )
如图,△ABC内接于⊙O,过BC的中点D作直线l∥AC,l与AB交于点E,与⊙O交于点G、F,与⊙O在点A处的切线交于点P,若PE=3,ED=2,EF=3,则PA的长度为( )| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com