
分析 (1)根据题意可得等量关系:剩下未改装车辆每天的燃料费=未改装车辆的数量×80,改装后的每辆出租车平均每天的燃料费比改装前的燃料费下降的百分比=1-(改装后的每辆车平均每天的燃料费÷80)×100%;
(2)根据(1)可得到出租车的总量和改装前后每天燃料费下降的百分点,可知一次性改装全部出租车可以从节省的燃料费中收回成本需要的天数=4000×100÷(100×80×40%).根据这个等量关系可列方程.
解答 解:(1)设公司第一次改装了y辆车,改装后的每辆出租车每天的燃料费比改装前的燃料费下降的百分数为x.
依题意得方程组:$\left\{\begin{array}{l}{y(1-x)×80=\frac{3}{20}(100-y)×80}\\{2y(1-x)×80=\frac{2}{5}(100-2y)×80}\end{array}\right.$,
化简得:$\frac{3}{20}$(100-y)=$\frac{1}{5}$(100-2y),
解得:$\left\{\begin{array}{l}{x=\frac{2}{5}=40%}\\{y=20}\end{array}\right.$,
20+20=40(辆).
答:公司共改装了40辆车,改装后的每辆出租车每天的燃料费比改装前的燃料费下降了40%.
(2)设一次性改装后,m天可以收回成本,则:
100×80×40%×m=4000×100,
解得:m=125.
答:125天后就可以从节省的燃料费中收回成本.
点评 此题主要考查了二元一次方程组的应用,关键是要弄清题意,根据题目给出的已知条件找出合适的等量关系,列出方程组,再求解.注意题目要求的是下降了多少百分点,要把计算出的数据转化为百分数.


科目:初中数学 来源: 题型:解答题
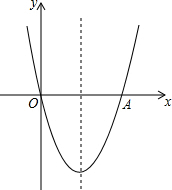 如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.
如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
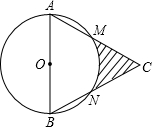 如图,等边△ABC边长为12cm,以AB为直径的⊙O分别交CA、CB于M、N两点,则图中阴影部分的面积是( )
如图,等边△ABC边长为12cm,以AB为直径的⊙O分别交CA、CB于M、N两点,则图中阴影部分的面积是( )| A. | 9$\sqrt{3}$-6π | B. | 18$\sqrt{3}$-6π | C. | 12$\sqrt{3}$-3π | D. | 12$\sqrt{3}$-6π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
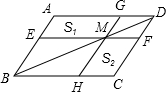 如图,过平行四边形ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的过平行四边形AEMG的面积S1与?HCFM的面积S2的大小关系是( )
如图,过平行四边形ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的过平行四边形AEMG的面积S1与?HCFM的面积S2的大小关系是( )| A. | S1>S2 | B. | S1=S2 | C. | S1<S2 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com