
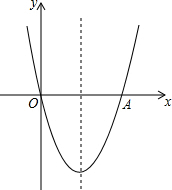
 如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.
如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.分析 (1)把抛物线的解析式化成顶点式即可求得对称轴;求得直线与坐标轴的交点坐标,即可证得直线和坐标轴围成的图形是等腰直角三角形,从而求得直线PQ与x轴所夹锐角的度数;
(2)分三种情况分别讨论根据已知条件,通过△OBE∽△ABF对应边成比例即可求得;
(3)①过点C作CH∥x轴交直线PQ于点H,可得△CHQ是等腰三角形,进而得出AD⊥PH,得出DQ=DH,从而得出PD+DQ=PH,过P点作PM⊥CH于点M,则△PMH是等腰直角三角形,得出PH=$\sqrt{2}$PM,因为当PM最大时,PH最大,通过求得PM的最大值,从而求得PH的最大值;由①可知:PD+PH≤6$\sqrt{2}$,设PD=a,则DQ$≤6\sqrt{2}$-a,得出PD•DQ≤a(6$\sqrt{2}$-a)=-a2+6$\sqrt{2}$a=-(a-3$\sqrt{2}$)2+18,当点P在抛物线的顶点时,a=3$\sqrt{2}$,得出PD•DQ≤18.
解答 方法一: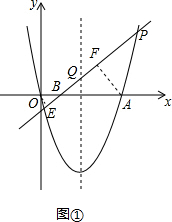 解:(1)∵y=x2-4x=(x-2)2-4,
解:(1)∵y=x2-4x=(x-2)2-4,
∴抛物线的对称轴是x=2,
∵直线y=x+m,
∴直线与坐标轴的交点坐标为(-m,0),(0,m),
∴交点到原点的距离相等,
∴直线与坐标轴围成的三角形是等腰直角三角形,
∴直线PQ与x轴所夹锐角的度数是45°,
故答案为x=2、45°.
(2)如图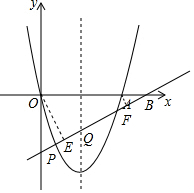
设直线PQ交x轴于点B,分别过O点,A点作PQ的垂线,垂足分别是E、F,显然当点B在OA的延长线时,S△POQ=$\frac{1}{3}$S△PAQ不成立;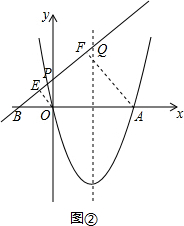
①当点B落在线段OA上时,如图①,
$\frac{{S}_{△POQ}}{{S}_{△PAQ}}$=$\frac{OE}{AF}$=$\frac{1}{3}$,
由△OBE∽△ABF得,$\frac{OB}{AB}$=$\frac{OE}{AF}$=$\frac{1}{3}$,
∴AB=3OB,
∴OB=$\frac{1}{4}$OA,
由y=x2-4x得点A(4,0),
∴OB=1,
∴B(1,0),
∴1+m=0,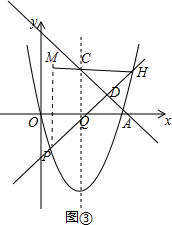
∴m=-1;
②当点B落在线段AO的延长线上时,如图②,同理可得OB=$\frac{1}{2}$OA=2,
∴B(-2,0),
∴-2+m=0,
∴m=2,
综上,当m=-1或2时,S△POQ=$\frac{1}{3}$S△PAQ;
(3)①过点C作CH∥x轴交直线PQ于点H,如图③,可得△CHQ是等腰三角形,
∵∠CDQ=45°+45°=90°,
∴AD⊥PH,
∴DQ=DH,
∴PD+DQ=PH,
过P点作PM⊥CH于点M,则△PMH是等腰直角三角形,
∴PH=$\sqrt{2}$PM,
∴当PM最大时,PH最大,
∴当点P在抛物线顶点处时,PM最大,此时PM=6,
∴PH的最大值为6$\sqrt{2}$,
即PD+DQ的最大值为6$\sqrt{2}$.
②由①可知:PD+DQ≤6$\sqrt{2}$,
设PD=a,则DQ$≤6\sqrt{2}$-a,
∴PD•DQ≤a(6$\sqrt{2}$-a)=-a2+6$\sqrt{2}$a=-(a-3$\sqrt{2}$)2+18,
∵当点P在抛物线的顶点时,a=3$\sqrt{2}$,
∴PD•DQ≤18.
∴PD•DQ的最大值为18.
方法二:
(1)略.
(2)过点A作x轴垂线,与直线PQ交于点D,设直线PQ与y轴交于点C,
∴C(0,m),D(4,4+m),
∵S△POQ=$\frac{1}{2}$(Qx-Px)(QY-CY),
S△PAQ=$\frac{1}{2}$(Qx-Px)(DY-AY),
∵$\frac{{S}_{△POQ}}{{S}_{△PAQ}}=\frac{1}{3}$,
∴$|\frac{{O}_{Y}-{C}_{Y}}{{D}_{Y}-{A}_{Y}}|=|\frac{0-m}{4+m}|=\frac{1}{3}$,
∴m1=2,m2=-1.
(3)①设P(t,t2-4t)(0<t<4),
∵KPQ=1,∴lPQ:y=x+t2-5t,
∵C(2,2),A(4,0),
∴lAC:y=-x+4,
∴DX=$\frac{-{t}^{2}+5t+4}{2}$,DY=$\frac{{t}^{2}-5t+4}{2}$,
∴Q(2,t2-5t+2),
∵PQ⊥AC,垂足为点D,
∴点Q关于直线AC的对称点Q′(-t2+5t+2,2),
欲使PD+DQ取得最大值,只需PQ′有最大值,
PQ′=$\sqrt{({t}^{2}-4t-2)^{2}+({t}^{2}-4t-2)^{2}}$=$\sqrt{2}|{t}^{2}-4t-2|$,
显然当t=2时,PQ′的最大值为6$\sqrt{2}$,
即PD+DQ的最大值为6$\sqrt{2}$,
②∵(PD+DQ)2≥4•PD•DQ,
∴PD•DQ≤$(\frac{PD+DQ}{2})^{2}$=$(\frac{6\sqrt{2}}{2})^{2}$=18,
∴PD•DQ的最大值为18.
点评 本题是二次函数的综合题,考查了抛物线的性质,直线的性质,三角形相似的判定和性质,难度较大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
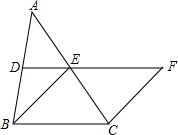 如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF
如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )| A. | BE=DF | B. | BF=DE | C. | AE=CF | D. | ∠1=∠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com