
【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为_____.

【答案】![]()
【解析】
设Q是AB的中点,连接DQ,先证得△AQD≌△AOE,得出QD=OE,根据点到直线的距离可知当QD⊥BC时,QD最小,然后根据等腰直角三角形的性质求得QD⊥BC时的QD的值,即可求得线段OE的最小值.
设Q是AB的中点,连接DQ,
∵∠BAC=∠DAE=90°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
∵AB=AC=2,O为AC中点,
∴AQ=AO,
在△AQD和△AOE中,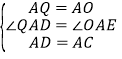
∴△AQD≌△AOE(SAS),
∴QD=OE,
∵点D在直线BC上运动,
∴当QD⊥BC时,QD最小,
∵△ABC是等腰直角三角形,
∴∠B=45°,
∵QD⊥BC,
∴△QBD是等腰直角三角形,
∴QD=![]() QB,
QB,
∵QB=![]() AB=1,
AB=1,
∴QD=![]() ,
,
∴线段OE的最小值是为![]() .
.
故选:B.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】下面是小东设计的“在三角形一边上求作一个点,使这点和三角形的两个顶点构成的三角形与原三角形相似”的尺规作图过程.
已知:△ABC.
求作:在BC边上求作一点P,使得△PAC∽△ABC.
作法:如图,
①作线段AC的垂直平分线GH;
②作线段AB的垂直平分线EF,交GH于点O;
③以点O为圆心,以OA为半径作圆;
④以点C为圆心,CA为半径画弧,交⊙O于点D(与点A不重合);
⑤连接线段AD交BC于点P.
所以点P就是所求作的点.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵CD=AC,
∴![]() = .
= .
∴∠ =∠ .
又∵∠ =∠ ,
∴△PAC∽△ABC( )(填推理的依据).

查看答案和解析>>
科目:初中数学 来源: 题型:
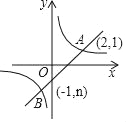
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A、B两点.
的图象交于A、B两点.
(1)利用图中的条件,求反比例函数和一次函数的解析式.
(2)求△AOB的面积.
(3)根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,∠ACD=∠B,那么下列判断中,不正确的是( )
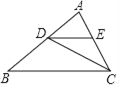
A. △ADE∽△ABC B. △CDE∽△BCD C. △ADE∽△ACD D. △ADE∽△DBC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为直角边在AD右侧作等腰直角三角形ADE,且∠DAE=90°,连接CE.

(1)如图①,当点D在线段BC上时:
①BC与CE的位置关系为 ;
②BC、CD、CE之间的数量关系为 .
(2)如图②,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若不成立,请你写出正确结论,并给予证明.
(3)如图③,当点D在线段BC的延长线上时,BC、CD、CE之间的数量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为![]() ,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
(1)求DE的长;
(2)过点EF作EF⊥CE,交AB于点F,求BF的长;
(3)过点E作EG⊥CE,交CD于点G,求DG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个全等的直角三角形 ABC 和 DEF 重叠在一起,其中∠A=60°,AC=1.固定△ABC 不动,将△DEF 进行如下操作:
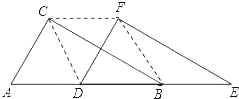
(1)如图,△DEF 沿线段 AB 向右平移(即 D 点在线段 AB 内移动),连接 DC、CF、FB,四边形 CDBF 的形状在不断的变化,但它的面积不变化,请求出其面积.
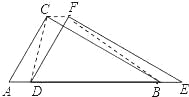
(2)如图,当 D 点移到 AB 的中点时,请你猜想四边形CDBF 的形状,并说明理由.
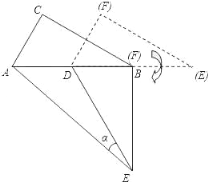
(3)如图,△DEF 的 D 点固定在 AB 的中点,然后绕 D 点按顺时针方向旋转△DEF,使 DF 落在 AB 边上,此时 F 点恰好与 B 点重合,连接 AE,请你求出 sinα的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,点E为AB边上的一点,点F为对角线BD上的一点,且EF⊥AB.若四边形ABCD为正方形.
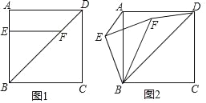
①如图1,请直接写出AE与DF的数量关系 ;
②将△EBF绕点B逆时针旋转到图2所示的位置,连接AE,DF,猜想AE与DF的数量关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小李上学用的自行车,型号是24英吋(车轮的直径为24英吋,约60厘米),为了防止在下雨天骑车时的泥水溅到身上,他想在自行车两轮的阴影部分两侧装上挡水的铁皮(两个阴影部分分别是以C、D为圆心的两个扇形),量出四边形ABCD中∠DAB=125°、∠ABC=115°,那么预计需要的铁皮面积约是( )

A. 942平方厘米 B. 1884平方厘米
C. 3768平方厘米 D. 4000平方厘米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com